Bernhard VALENTINI
A three-dimensional constitutive model for concrete and its application to large scale finite element analyses
2011
- Kurzfassung auf Deutsch
Für diese Dissertation wurde Herrn Dr. Valentini an der TU Wien der FCP-Innovationspreis 2011 "für nachhaltige Entwicklungen im Ingenieurbau" der Firma FCP – Fritsch, Chiari & Partner ZT GmbH verliehen.
Zudem wurde Herrn Dr. Valentini für diese Dissertation der Scientific Computing Thesis Award 2011 der Universität Innsbruck verliehen.
Abstract
This thesis deals with the critical evaluation, comparison and further development of three-dimensional constitutive models for concrete, the implementation of an enhanced constitutive model for concrete into a finite element analysis program system, the validation of the concrete model and its application to three-dimensional large scale finite element analyses. To this end, the solution procedure of the stress update at the integration point level has to be robust, accurate and efficient. Hence, different solution procedures for the stress update, based on an implicit integration algorithm, are compared and verified with respect to their robustness, accuracy and efficiency at the integration point level and the structural level, respectively.
The investigated constitutive models consist of a single-surface plasticity model which was developed by Etse [1992], denoted as Extended Leon model, an enhanced version of the Extended Leon model, proposed by Pivonka [2001], and a constitutive model based on the combination of the theories of plasticity and continuum damage mechanics, proposed by Grassl [2006]. In this thesis the latter model is referred to as Modified Leon model. Each of these constitutive models was developed for describing the nonlinear hardening and nonlinear softening behaviour of concrete under uniaxial, biaxial and triaxial loading. To provide a better representation of experimental results, in particular for compressive loading and combined tensile-compressive loading, the softening law of the Modified Leon model is enhanced by the author of this thesis. To guarantee objectivity of the material models with regard to the finite element mesh size, a regularization scheme for the applied constitutive models is presented.
Three different solution procedures for the stress update, based on the Backward Euler method, are implemented and assessed in the framework of the present thesis. They comprise the Newton method, a damped Newton method proposed by Deuflhard [2004] and a substepping scheme developed by Perez-Foguet [2001]. In addition, an adaptive substepping strategy with error control is presented. The robustness, accuracy and efficiency of the solution procedures are compared by evaluating the convergence, the relative errors and the time required for the computation of the stresses for different sets of trial stress states.
The constitutive models are validated by numerical simulations of small scale tests. To this end, uniaxial tensile tests and uniaxial, biaxial and triaxial compression tests of plain concrete are simulated numerically. The results of the analyses predicted by the enhanced version of the Extended Leon model, the Modified Leon model and the enhanced version of the Modified Leon model are compared to the experimental results. The validation of the enhanced version of the Modified Leon model and the verification of the implemented solution procedures at the structural level are shown by three-dimensional numerical simulations of four small scale benchmark tests of plain and reinforced concrete specimens, subjected to different types of loading (cf. figure). Finally, the applicability of the enhanced version of the Modified Leon model to a large scale three-dimensional finite element analysis is demonstrated by the ultimate load analysis of a model test of Zillergründl arch dam, which was conducted on the scale of 1:200. The comparison of the predicted and measured structural response shows the capabilities of the developed numerical model.
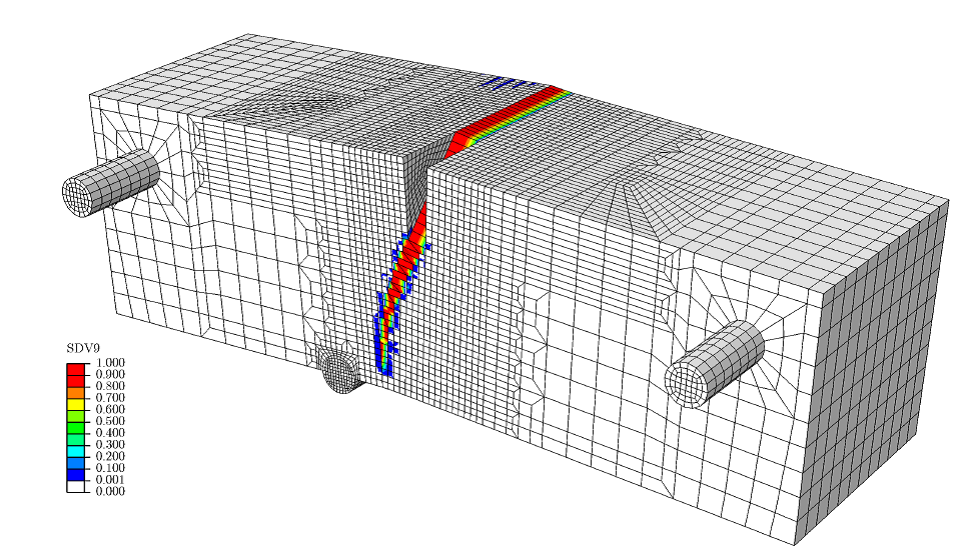
Computed crack pattern at failure for a torsional shear fracture test
Im Rahmen dieser Dissertation werden dreidimensionale konstitutive Gesetze für Beton bewertet, miteinander verglichen und weiterentwickelt. Dies sind ein Einflächenplastizitätsmodell, welches von Etse [1992] entwickelt wurde und als Extended Leon model bezeichnet wird, eine erweiterte Version dieses Modells von Pivonka [2001] und ein kombiniertes Schädigungs-Plastizitätsmodell, welches in Grassl [2006] vorgestellt wurde. Im Rahmen dieser Arbeit wird letzteres Modell als Modified Leon model bezeichnet. Jedes dieser drei Materialmodelle wurde entwickelt, um das nichtlineare Verfestigungs- und Entfestigungsverhalten von Beton unter einaxialer, biaxialer und triaxialer Beanspruchung wiederzugeben. Um das Materialverhalten von Beton, insbesondere unter einaxialer Druckbeanspruchung und kombinierter Druck-Zugbeanspruchung, besser abbilden zu können, wurde vom Autor dieser Arbeit das Entfestigungsgesetz des konstitutiven Modells von Grassl [2006] erweitert. Des Weiteren wird ein Schema zur Regularisierung der Materialentfestigung präsentiert, welches die Objektivität der Ergebnisse, unabhängig von der Größe der finiten Elemente, garantiert.
Zur Implementierung der weiterentwickelten Materialmodelle für Beton in ein finite Elemente Programmsystem muss der Lösungsalgorithmus für die Aktualisierung des Spannungstensors auf Integrationspunktebene robust, genau und effizient sein. Drei verschiedene Lösungsalgorithmen, basierend auf dem Rückwärts-Euler-Verfahren, werden im Rahmen dieser Arbeit implementiert und bewertet. Dies sind das Newton-Verfahren, ein gedämpftes Newton-Verfahren, welches von Deuflhard [2004] vorgeschlagen wurde, und ein mehrstufiges Verfahren, welches in Perez-Foguet [2001] angewendet wurde. Zusätzlich wird eine Strategie zur adaptiven Steuerung des mehrstufigen Verfahrens und eine Strategie zur Kontrolle der Fehler der Spannungsintegration präsentiert. Die Robustheit, Genauigkeit und Effizienz der verschiedenen Lösungsstrategien wird anhand der Auswertung der Konvergenz, der relativen Fehler und der benötigten Zeit für die Berechnung der Spannungen für verschiedene Sets von Prädiktorspannungen verglichen.
Die einzelnen konstitutiven Modelle werden durch die Nachrechnung von kleinmaßstäblichen Versuchen validiert. Zu diesem Zweck werden einaxiale Zugversuche und einaxiale, biaxiale und triaxiale Druckversuche von unbewehrten Betonprobekörpern numerisch simuliert. Die mittels der erweiterten Version des Extended Leon model, des Modified Leon model und der hier erweiterten Version des Modified Leon model prognostizierten Resultate werden mit experimentellen Ergebnissen verglichen. Die Validierung der erweiterten Version des Modified Leon model und die Verifizierung der implementierten Lösungsalgorithmen auf Strukturebene erfolgen durch dreidimensionale numerische Berechnungen von vier kleinmaßstäblichen Benchmark-Tests aus unbewehrtem bzw. bewehrtem Beton (siehe Abbildung). Abschließend wird die Anwendbarkeit der erweiterten Version des Modified Leon model für große dreidimensionale finite Elemente Berechnungen anhand der Traglastanalyse eines im Maßstab 1:200 durchgeführten Modellversuchs der Gewölbestaumauer Zillergründl demonstriert. Durch den Vergleich der prognostizierten und experimentell bestimmten Strukturantwort wird die Leistungsfähigkeit des entwickelten numerischen Modells nachgewiesen.
