Roman KOHLER
Numerical Modelling of Partially Saturated Soils in the Context of a Three Phase FE Formulation
2006
- Kurzfassung auf Deutsch
Abstract
The present thesis deals with the development and validation of a constitutive model for the mechanical behavior of partially saturated soils and its implementation into a three-phase FE-formulation. Such numerical models can be applied to the simulation of a broad range of geotechnical problems covering consolidation, drying and wetting of soils under atmospheric conditions as for instance after the impoundment of an earth dam as well as dewatering by means of compressed air e.g. in the context of tunneling below the groundwater table.
A multi-surface plasticity model for drained conditions serves as starting point for the development of the material model. In order to investigate different approaches for the description of the stress state controlling the mechanical behavior of partially saturated soils the basic model is reformulated in terms of an effective stress tensor for partially saturated soils on the one hand as well as it is extended in terms of two stress state variables on the other hand. The latter is obtained by considering the evolution of the shear strength and the stiffness in terms of matric suction. By comparing numerical results to experimental data it is shown that only the extended material model formulated in terms of two stress state variables is able to reproduce the behavior of partially saturated soils, e.g. the collapse on wetting (cf. figure).
Two different approaches of the extended material model are suggested and investigated. The first one relies on the application of the net stress tensor and matric suction as independent stress state variables whereas the second one relies on the use of the Bishop stress tensor in combination with matric suction as stress like plastic internal variable. The extended models are validated by simulating a series of suction controlled experiments numerically.
Both versions of the extended model are able to adequately predict the behavior of soils at partially saturated conditions but only the second one allows a straightforward transition to the effective stress tensor for fully water saturated soils in the context of a FE-formulation, as shown by the numerical simulation of a consolidation problem.
A return mapping algorithm for the proposed material models is derived by applying an implicit backward Euler integration scheme and the tensors of material tangent moduli are presented. In contrast to classical elasto-plastic material models in terms of a single stress state variable a second tensor of material tangent moduli (with respect to the matric suction) is obtained.
The proposed FE-model is validated by means of a numerical investigation comparing the numerical results of example problems to analytical solutions and experimental data documented in the literature. The numerical study contains the simulation
(i) of a consolidation problem,
(ii) of a laboratory experiment on a soil column subjected to cycles of drainage and wetting and
(iii) a coupled solid-fluid analysis of water flow during and after the impoundment of an earth dam.
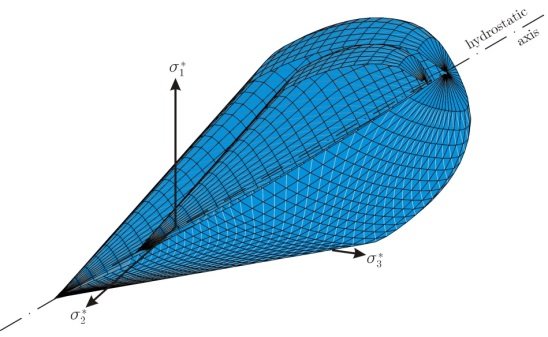
Sliced yield surfaces for two different values of matric suction in the principal net stress space
Die vorliegende Arbeit beschäftigt sich mit der Entwicklung und Verifizierung eines Werkstoffgesetzes zur Beschreibung des mechanischen Verhaltens teilgesättigter Böden und dessen Implementierung in eine Drei-Phasen FE-Formulierung. Solche numerischen Modelle eignen sich für die Simulation einer Vielzahl von geotechnischen Problemstellungen wie Konsolidierung, Be- und Entwässerung von Böden unter atmosphärischen Bedingungen wie der Durchströmung von Erddämmen und Entwässerung mittels Druckluft z.B. im Rahmen von Tunnelvortrieben unterhalb des Grundwasserspiegels.
Ausgehend von einem Mehrflächen-Plastizitätsmodell für drainierte Bedingungen werden unterschiedliche Ansätze für die Beschreibung des Spannungszustandes teilgesättigter Böden untersucht und verglichen indem das zugrundeliegende Modell einerseits in Abhängigkeit eines effektiven Spannungstensors für teilgesättigte Böden umformuliert wird und andererseits auf der Basis von zwei Spannungs-zustandsvariablen erweitert wird. Letzteres erfolgt durch die Berücksichtigung der Entwicklung der Scherfestigkeit sowie der Steifigkeit mit zunehmender Kapillarspannung. Anhand der Nachrechnung von Versuchen wird gezeigt, dass nur das erweiterte Materialmodell eine adäquate Modellierung des Verhaltens teilgesättigter Böden, wie z.B. die irreversible Volumenabnahme bei Bewässerung, erlaubt (siehe Abbildung).
In dieser Arbeit werden zwei Versionen des in zwei Spannungsvariablen formulierten Modells vorgeschlagen und untersucht. Die erste ist gekennzeichnet durch die Verwendung der Nettospannungen und der Kapillarspannung als unabhängige Spannungszustandsvariablen während für die zweite die Bishop-Spannungen in Kombination mit der Kapillarspannung als plastische interne Variable verwendet werden. Die Validierung der Materialmodelle erfolgt anhand einer in der Literatur wiedergegebenen Versuchserie mit verschiedenen Werten der Kapillarspannung. Während beide Versionen des erweiterten Materialmodells für die Modellierung unter teilgesättigten Bedingungen geeignet sind, erlaubt nur letztere einen automatischen Übergang zum Konzept der effektiven Spannungen für wassergesättigte Böden im Rahmen der FE-Formulierung, wie anhand eines Konsolidierungsbeispieles gezeigt wird.
Basierend auf der Anwendung der impliziten Eulerschen Rückwärtsmethode wird ein Projektionsverfahren für die vorgeschlagenen Materialmodelle abgeleitet und die elasto-plastischen Materialtensoren werden ermittelt. Im Gegensatz zu klassischen Materialmodellen wird ein zweiter Materialtensor in Bezug auf die Kapillarspannung erhalten.
Die Verifikation des entwickelten FE-Modells erfolgt anhand der numerischen Simulation von Beispielen und Vergleichen der numerischen Ergebnisse mit analytischen Lösungen bzw. Versuchsdaten. Die numerische Studie umfasst die Simulation
(i) eines Konsolidierungsproblems,
(ii) eines Laborversuches zur Ent- und Bewässerung einer Bodensäule und
(iii) des Verhaltens eines Erddamms während und nach dem Einstau.
