Christian FEIST
A numerical model for cracking of plain concrete based on the strong discontinuity approach
2004
- Kurzfassung auf Deutsch
Abstract
The present thesis is devoted to the development of a family of finite elements which are capable to resolve fracture processes in plain concrete structures. From the mathematical point of view the formation of discrete cracks can be considered as the development of discontinuity surfaces exhibiting displacement jumps. The strong discontinuity kinematics offer an appropriate description of the kinematics of solids crossed by such discontinuity surfaces.
The presented numerical model is formulated within the framework of the strong discontinuity approach (SDA) employing the concept of elements with embedded discontinuities. These elements allow discontinuity surfaces to cross spatial discretizations of solids in arbitrary ways, thus making adaptive procedures dispensable. The numerical model is formulated for quasi-static, monotonic loading adopting the hypothesis of small displacements and small strains. In view of the application to simulations of concrete the RANKINE failure criterion is employed. The presented elements are implemented for two- and three-dimensional problems in a commercial finite element code.
The presented model is further based on the fixed crack concept assuming the geometrical representation (locus and orientation) of the discontinuity surface to be fixed with respect to pseudo-time. It is shown that in this case the basic SDA model exhibits mesh-dependence in the sense that the numerical representation of a crack is attracted by mesh lines. Tracking strategies allow to enforce a continuous crack path and thus to overcome mesh dependence of the model. A partial domain tracking strategy that is capable to resolve fracture problems involving multiple cracks as well as three-dimensional crack propagation is presented. With respect to the determination of the crack propagation direction the model is refined by using a nonlocal averaging procedure.
The proposed model is validated by means of the numerical simulation of well-known laboratory tests. Applicability to large scale analyses is demonstrated by the simulation of a gravity dam. The simulation of dams motivates an extension of the numerical model with respect to the consideration of the fluid pressure in opening cracks. A simple but efficient numerical model accounting for this effect is proposed.
In addition to experiments documented in the literature an extensive experimental work is conducted. Tests on two- and three-dimensionally stressed beams serve as a means for the verification of the SDA-formulation.
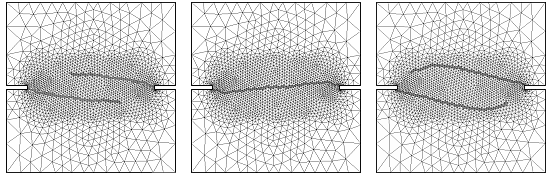
Computed crack paths for mixed mode fracture tests with different load paths
Die vorliegende Arbeit ist der Entwicklung einer Familie von finiten Elementen zur Simulation des Versagens unbewehrter Betonstrukturen infolge des Reißens des Werkstoffes gewidmet. Die Ausbildung eines diskreten Risses kann aus mathematischer Sicht als Bildung einer durch eine Unstetigkeit im Verschiebungsfeld gekennzeichneten Diskontinuitätsfläche angesehen werden. Die Beschreibung der Kinematik eines Festkörpers, durch welchen eine solche Diskontinuitätsfläche verläuft, erfolgt mit Hilfe des Konzepts der Kinematik einer starken Diskontinuität (strong discontinuity kinematics). Das vorgestellte numerische Modell basiert auf der Methode der starken Diskontinuitäten (strong discontinuity approach -- SDA) und ist im Rahmen des Konzepts der Elemente mit eingebetteten Diskontinuitäten (elements with embedded discontinuities) formuliert. Diese Elemente erlauben die Abbildung von Diskontinuitätsflächen, welche eine gewählte räumliche Diskretisierung in nahezu beliebiger Form durchschneiden können. Somit kann auf die Anwendung aufwändiger adaptiver Methoden verzichtet werden. Das numerische Modell ist für quasi-statische Aufgabenstellungen unter der Annahme kleiner Verschiebungen und kleiner Verzerrungen für monotone Belastungsszenarien formuliert. Als Bruchhypothese wird das Kriterium von RANKINE verwendet. Die vorgestellten Elemente sind für zwei- und dreidimensionale Probleme in ein kommerzielles FE-Paket implementiert.
Das numerische Modell basiert weiters auf dem Konzept mit unveränderlichen Rissflächen (fixed crack concept). Es zeigt sich, dass das SDA-Modell in seiner Grundform netzabhängige Lösungen liefert, insofern als die numerische Auflösung eines diskreten Risses durch die Netztopologie beeinflusst wird. Rissverfolgungsstrategien (tracking strategies) bieten die Möglichkeit, über benachbarte Elemente stetige Diskontinuitätsflächen zu beschreiben, um somit jene Netzabhängigkeit zu beseitigen. Ein neuer Rissverfolgungsalgorithmus, welcher sowohl die Behandlung von Problemen mit mehreren Rissen als auch von Problemen mit räumlichen Rissflächen erlaubt, wird vorgestellt. Überdies wird die Bestimmung der Ausbreitungsrichtung von Rissflächen durch ein nichtlokales Mittelungsverfahren (nonlocal averaging) verbessert.
Das numerische Modell wird an Hand von aus der Literatur bekannten Laborversuchen verifiziert. Die anschließende Analyse einer Gewichtsstaumauer beweist die Anwendbarkeit des Modells auf Simulationen großer Strukturen. Traglastuntersuchungen von Staumauern geben auch den Anstoss zu Betrachtungen hinsichtlich der Berücksichtigung des Wasserdrucks in sich öffnenden Rissen. Davon ausgehend wird eine Erweiterung des SDA-Modells bezüglich dieses Effektes vorgeschlagen.
Zusätzlich zu den aus der Literatur bekannten Versuchen wird auch ein eigenes Versuchsprogramm durchgeführt und dokumentiert. Die darin enthaltenen Versuche an gekerbten Betonbalken mit dreidimensionalen Belastungszuständen sind von besonderem Wert für die Verifizierung der dreidimensionalen SDA-Formulierung.
