Gerhard ÖTTL
Numerische Simulation des Tunnelvortriebs unter Grundwasser mit Hilfe von Druckluft
2003
Kurzfassung
Das Ziel der Arbeit besteht in der Entwicklung eines numerischen Modells zur Simulation des Tunnelvortriebes unter Grundwasser mit Berücksichtigung der Grundwasserverdrängung im Bereich der Ortsbrust durch Druckluft. Die Verformungen im Boden werden bei einem derartigen Problem sowohl durch die Entwässerung des Bodens als auch durch den Tunnelvortrieb verursacht.
Insbesondere im städtischen Bereich spielt die Minimierung der Oberflächensetzungen während des Tunnelvortriebes eine zentrale Rolle um Schäden an der bestehenden Bebauung zu vermeiden. Beim Auffahren eines Tunnels unterhalb des Grundwasserspiegels ist eine Verdrängung des Grundwassers im Bereich der Ortsbrust notwendig. Der Einsatz von Druckluft scheint dafür eine geeignete Methode zu sein, da die Luftströmung die Deformationen zufolge der Entwässerung des Bodens und des Tunnelausbruchs vermindert. Die nachstehende Abbildung zeigt das Prinzip des Tunnelvortriebes unter Druckluft.
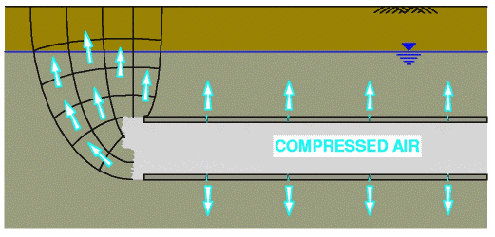
Prinzip des Tunnelvortriebes unter Druckluft
Für die gegebene Aufgabenstellung gibt es prinzipiell zwei verschiedene Lösungsmöglichkeiten, eine ungekoppelte und eine gekoppelte. Im Gegensatz zur ungekoppelten Lösung erlaubt ein gekoppelter Ansatz, wie er in der gegenständlichen Arbeit zur Anwendung gelangt, die Berücksichtigung der Interaktionen zwischen dem Problem der Entwässerung des Bodens und dessen Verformungen auf physikalisch korrekte Weise.
Einen elementaren Bestandteil dieses gekoppelten numerischen Modells zur Simulation des Tunnelvortriebes unter Druckluft bildet eine 3-Phasen Formulierung für den Boden, worin dieser aus einem verformbaren Korngerüst und den beiden Fluidphasen Wasser und Druckluft besteht. Die mathematische Beschreibung eines 3-Phasen Mediums basiert auf den Ansätzen der Mischungstheorie unter Berücksichtigung von sogenannten Mittelungsprozessen.
Für die numerische Lösung des 3-Phasen Problems im Rahmen der Methode der Finiten Elemente (FEM) wird die Formulierung in ein FE-Programm implementiert. Die Verifikation des FE-Codes sowie des physikalischen Modells erfolgt durch die numerische Simulation verschiedener Labor- und Feldversuche.
Die beschriebene Arbeit ist Inhalt des Teilprojektes Numerische Simulation des Tunnelvortriebes unter Berücksichtigung der Grundwasserverdrängung durch Druckluft des österreichischen Forschungsschwerpunktes (FSP) Numerische Simulation im Tunnelbau.
