Hypoplasticity

Genealogy of Hypoplasticity

Hippo

Hypoplasticity illustrated in terms of Elastoplasticity

J.J. Nader, 1998

One of the main features of soil behaviour, observed in engineering works and in controlled laboratory tests, is the ocurrence of irreversible deformation. In many practical problems it is admissible to neglect the more or less pronounced time dependent character of soil deformation and treat soils as rate-independent materials. To describe soil behaviour as a rate-independent material the most used and known framework is the theory of Elastoplasticity. Since the end of the 50´s, following the pioneer Cam-Clay, new elastoplastic models have been developed with increasing complexity in order to represent soil behaviour. An alternative to elastoplastic models for the mathematical description of soil mechanical behaviour appeared in 1977, created by Kolymbas in his doctoral thesis at the University of Karlsruhe, Germany, and was named Hypoplasticity. With a single constitutive equation, inspired by modern rational mechanics, without recourse to yield or potential surfaces, important phenomena of soil mechanical behaviour can be represented.

We aim in this brief communication at presenting Hypoplasticity taking advantage of the reader's basic knowlegde of Elastoplasticty. A comparison between the two above mentioned theories, restricted by the introductory character of this text, will also be done.

A fundamental ingredient of elastoplastic models is the yield surface in the stress space, which is introduced by a yield function. The yield surface, associated to a particular state of the material, bounds, in the stress space, a region called elastic domain. The most used models are the isotropic-hardening elastoplastic ones where the plastic state is characterized by a single scalar called hardening parameter.

We now introduce two terms extensively used here: elastic and plastic regime.

The regime is said to be elastic when only reversible (elastic) deformation occurs. This reversibility is detected in a stress cycle. In this case the plastic state of the material does not change.

If the deformation is not totally reversible the regime is elastoplastic and the irreversible part of the deformation is called plastic. When the regime, initially elastic, becomes elastoplastic the material yields becoming more deformable.

Since there are more than one definition of stress and deformation tensors, each particular elastoplastic model must define which of them are being employed. For soils we employ, in most modern models, the Cauchy stress T and the stretching D (the symmetric part of the spatial velocity gradient) as a measure of the rate of deformation.

We now proceed giving the definition of elastic and elastoplastic regime in terms of stress. This will provide a relation between stress and rate of deformation.

If the stress to which the material is subject corresponds to a point located within the elastic domain, we specify that, at this instant, the regime is elastic whatever the stress change is. During a certain time interval the stress path remains within the elastic domain and the corresponding regime is elastic. In elastic regime the constitutive equation belongs to Hypoelasticity: T°=h(T,D), wherein T° is the Jaumann derivative of T, also called co-rotated stress rate and the function h(T,D) is isotropic with respect to both arguments and linear and homogeneous of degree 1 in D. To emphasize the linearity in D, we agree to write T°=h(T)[D]. In Elastoplasticity the inverse relation is more usually employed: D=L(T)[T°], with L(T)=h-1(T) (only invertible relations are considered).

We have just considered the case when the stress point is within the elastic domain. Now let us describe what happens if the stress point lies initially on the yield surface. If the stress increment is directed inwards the elastic domain or it is tangent to the yield surface, the regime is elastic, and, so, the same hypoelastic equation relates stretching, stress and stress rate. On the other hand, an elastoplastic regime begins if the stress increment points to the outer region. In its motion outwards the present elastic domain, the stress point enlarges or displaces continuously the yield surface, in such a way that it remains on the yield surface, i.e., at any instant of an elastoplastic regime the stress point is on the yield surface correspondent to that plastic state. Thus the stress point is never outside the region limited by the current yield surface. Well, the constitutive relation for the elastoplastic regime has not yet been mentioned. As an axiom it is stated that the stretching, at any instant of an elastoplastic regime, is the sum of two parts. One is the elastic stretching De, given by the same hypoelastic equation valid for elastic regimes (De=L(T)[T°]); and the other is the plastic stretching Dp.

The constitutive equation relating the plastic stretching, the stress, the stress rate and the state parameters must be specified. Once more a linear relation, this time between plastic stretching and stress rate for each value of the stress, is used. If a continuous material response is to be represented, the plastic stretching for a stress rate tangent to the yield surface must vanish. Thus, it can be shown that the linear relation between plastic stretching and stress rate must have a particular form: the linear function is an inner product of the stress rate and a tensor normal to the yield surface. The tensor n(T), with unitary norm and normal to the yield surface, is employed in the equation. In other words, interpreting it geometrically, it is the scalar projection of the stress rate onto the normal to the yield surface that enters the plastic constitutive equation; if that projection is null, i.e., if the stress rate is tangent to the yield surface, then the plastic stretching is null as well. So the plastic stretching tensor equals that inner product times a tensor function P(T) of the stress and the state parameters, which gives the direction of the plastic stretching: Dp=(n(T):T')P(T), in which T' is the time derivative of the stress tensor T. As n(T):T' is equal to n(T):T°, we may write Dp=(n(T):T°)P(T). The tensor function P(T) is, in many theories, a multiple of the normal to the yield surface n(T) at the corresponding stress point: P(T)=b(T)n(T). This particular form can be either stated a priori or deduced from an axiom regarding the stress power (Drucker's axiom) and, anyway, it is called the normality condition: an allusion to the orthogonality between the plastic stretching and the yield surface at the current stress point. It is important to emphasize that the direction of the plastic stretching does not depend on the direction of the stress rate.

Thus, repeating the main points, we have:

In elastic regime: D=L(T)[T°].

In elastoplastic regime: D=De+Dp=L(T)[T°]+(n(T):T°)P(T)

In this way one can model irreversible deformation. As an example, if the stress T is on the yield surface and a stress rate T' is applied causing elastoplastic regime, the stretching is given by the sum of elastic and plastic ones. On the other hand, if the stress rate is -T', leading to elasticregime, the stretching is the negative of the elastic stretching of the previous case.

The hypoplastic constitutive equation relates Cauchy stress T, the Jaumann derivative of T and the stretching D in the following manner: T°=h(T,D). At this early point we may start the confront with Elastoplasticity. There, at first, yield function and the corresponding surface, loading criterion and two constitutive equations are prescribed. Here the starting point is simpler: one equation.

The function h(T,D) must be isotropic with respect to both arguments to obey the principle of objectivity (material frame-indifference), and so, making use of a representation theorem of tensor algebra, it can be written as:

h(T,D)=f11+f2T+f3D+f4T2+f5D2+f6(TD+DT)+f7(TD2+D2T)+f8(T2D+DT2)+f9(T2D2+D2T2)

in which fi are scalar functions of joint invariants of T and D.

It is clear that for each particular stress T, the relation between T° and D, unlike the hypoelastic case, is non-linear. It is this non-linearity that makes possible the representation of irreversible deformation with a single equation.

When only rate-independent behaviour is to be represented, another restriction is imposed to the above equation: h(T,D) must be positively homogeneous of degree 1 in D.

Since 1977 special cases of the general rate-independent equation have been proposed in order to describe soil behaviour as observed in laboratory tests. All those cases are particular instances of an equation in which T° is given by the sum of two parts; the first one is linear in D (hypoelastic) and the second one is non-linear: T°=L(T)[D]+Q(T,D).

Although in Hypoplasticity there is no previous definition of different regimes, we now show how irreversible deformation is naturally taken into account. For the material to suffer a stretching D, the stress rate T°=L(T)[D]+Q(T,D) is required. If the stretching is -D, the corresponding stress rate is not -T°, but T°=-L(T)[D]+Q(T,-D), with Q(T,-D) different from -Q(T,D) in general, due to the non-linearity (it is strictly positively homogeneous). In Elastoplasticity the difference in behaviour has to be done with two linear functions.

Until today the most used special case of the general hypoplastic non-linear relation is T°=L(T)[D]+N(T)||D||, in which the norm ||D|| is responsible for the non-linearity. Note that the direction of the non-linear part does not depend on D.

For a direct comparison with elastoplastic equations the relation between T° and D can be inverted, giving, restricting the discussion to the just mentioned special case,

D=L-1(T)[T°]-L-1(T)[N(T)]a(T,T°),

where the scalar valued function a(T,T°) equals ||D|| (||D||=a(T,T°), never negative). Defining M(T)=L-1(T)[N(T)] in order to get a more compact equation, it becomes D=L-1(T)[T°]-a(T,T°)M(T). This particular form of hypoplastic equation resembles the one for the stretching in elastoplastic regime: the first part is linear and its direction and magnitude depends on T°; the direction of the second part does not depend on the direction of T°. A difference is that in Elastoplasticity the second part is linear in T°, whereas in hypopasticity it is non-linear.

Note the different material response when T° or -T° is applied. For T° the corresponding D is D=L-1(T)[T°]-a(T,T°)M(T), but, for -T°, it gives D=-L-1(T)[T°]-a(T,T°)M(T).

In Elastoplasticity, yield function and material state parameters define the yield surface, which bounds the elastic domain. As we have already seen, within the elastic domain only elastic deformation occurs, the material is more rigid. The yield surface is a kind of material memory. In Hypoplasticity there is no yield function, no elastic domain. All past information is concentrated in the current stress. Indeed, there are today new versions of hypoplastic equations involving the void ratio and a structural tensor that are more sensible to past deformation history.

Equations of the Hypoplastic Law

Wolfgang Fellin
1999-10-01

Abstract:

This is a very brief summary of the Hypoplastic Constitutive Law (a collection of equations). First some basic definitions are given. Then the equations and parameters of two Versions of the Hypoplastic law are shown.

Details on this item can be obtained from references [3].

A motion consists of translation, rotation and deformation. A material point with the material (or initial or LAGRANGE) coordinates Xα(α = 1,2,3) moves into a position with the spatial (or EULER) coordinates xi(i=1,2,3). Thus, the motion is described by the function x = χ(X,t). Using a less exact notation we can write x = x(X,t) . The deformation gradient is defined as

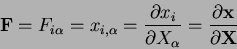
Deformation Funktion

EULER's stretching tensor D is obtained as the symmetric part of the velocity gradient 

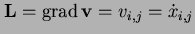
Formel Stretching L

Thus we have

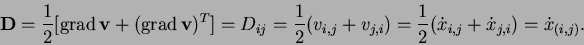
Formel Stretching D

CAUCHY's spin tensor is obtained as the antimetric part of the velocity gradient:

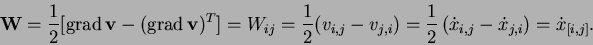
Formel Stretching W

Cutting a body reveals the internal forces acting within it. Let us consider a particular point of the cutting surface with the unit normal n and the stress vector (i.e. areal density of force) t . Both vectors are connected by the linear transformation T:

t = Tn

T is the CAUCHY stress tensor. By lack of couple stresses the stress tensor T is symmetric.

The components of T are denoted by Tij•:

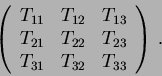
Cauchy stress
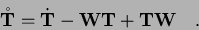
Objective time rate Funktion T

T

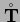
is the co-rotational or ZAREMBA or JAUMANN stress rate.

T

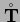
is the stress change that results solely from the deformation of the considered material, whereas any apparent parts (due to rotations of the observer or of the reference frame) are removed.

This version was propesed in references [5].

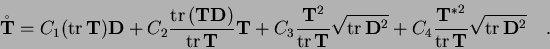
4 Funktion T

with

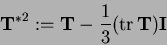
4 Funktion T2

The parameters for Karlsruhe sand are: 

DensityC1C2C3C4reference
loose -33,3 -308,4 -306,8 321,3 [5]
dense (e0 = 0,55) -110,15 -963,73 -877,19 1226,2 [1]
loose (e0 = 0,76) -69,23 -670,72 -653,26 690,9 [1]

This version was propesed in references [4].

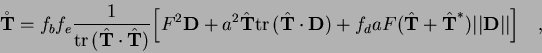
Version VON WOLFFERSDORF Funktion 18

with

Version VON WOLFFERSDORF Funktion 19

and

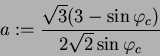
Version VON WOLFFERSDORF Funktion 20

The factor F is 

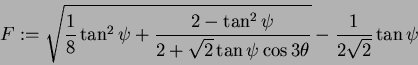
Version VON WOLFFERSDORF Funktion 21

with

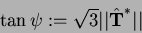
Version VON WOLFFERSDORF Funktion 22

and

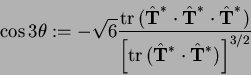
Version VON WOLFFERSDORF Funktion 23

The other scalar factors are:

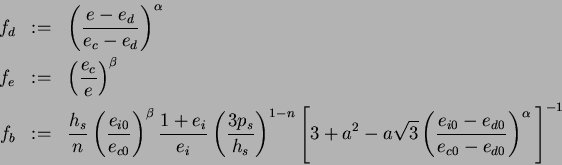
Version VON WOLFFERSDORF Funktion 24

 with

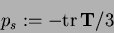
Version VON WOLFFERSDORF Funktion 25

The void ratios must fullfill

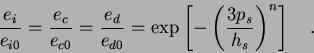
Version VON WOLFFERSDORF Funktion 26

This hypoplastic law has 8 parameters: the critical friktion angle φc, die granular hardness hs, die void ratios ei0, ec0 and ed0 the exponents n and β. They can be easily determined from simple index and/or element tests [2].

The parameters for different materials are [2]:

Materialφc [°]hs [MPa]ned0ec0ei0αβ
Toyoura sand 30 2600 0,27 0,61 0,98 1,10 0,18 1,00
Hochstetten sand 33 1500 0,28 0,55 0,95 1,05 0,25 1,50
Schlabendorf sand 33 1600 0,19 0,44 0,85 1,00 0,25 1,00
Hostun sand 31 1000 0,29 0,61 0,91 1,09 0,13 2,00
Karlsruhe sand 30 5800 0,28 0,53 0,84 1,00 0,13 1,05
Zbraslav sand 31 5700 0,25 0,52 0,82 0,95 0,23 1,00
Ottawa sand 30 4900 0,29 0,49 0,76 0,88 0,10 1,00
Ticino sand 31 5800 0,31 0,60 0,93 1,05 0,20 1,00
SLB sand 30 8900 0,33 0,49 0,79 0,90 0,14 1,00
Hochstetten gravel 36 32000 0,18 0,26 0,45 0,50 0,10 1,80
plastics 32 110 0,33 0,53 0,73 0,80 0,08 1,00
wheat 39 20 0,37 0,57 0,84 0,95 0,02 1,00

1

E. BAUER. Zum mechanischen Verhalten granularer Stoffe unter vorwiegend ödometrischer Beanspruchung. Publ. Series of Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, No. 130, 1992.

2

I. HERLE. Hypoplastizität und Granulometrie von Korngerüsten. Publ. Series of Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, No. 142, 1997.

3

D. KOLYMBAS. Introduction to Hypoplasticity. Advances in Geotechnical Engineering, Number 1. A.A. Balkema, 1999

4

P.-A. VON WOLFFERSDORFF. A hypoplastic relation for granular materials with a predefined limit state surface. Mechanics of Cohesive-Frictional Materials, 1:251-271, 1996.

5

W. WU. Hypoplastizität als mathematisches Modell zum mechanischen Verhalten granularer Stoffe. Publ. Series of Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, Vol. 129, 1992.

Equations of the Hypoplastic Law

This document was generated using the LaTeX2HTML translator Version 98.1 release (February 19th, 1998)

Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -t Equations of the Hypoplastic Law -split 4 -toc_depth 4 -local_icons -show_section_numbers hypo_www.

The translation was initiated by Wolfgang Fellin on 1999-10-01

  1. E. Bauer. Zum mechanischen Verhalten granularer Stoffe unter vorwiegend ödometrischer Beanspruchung. Veröffentlichung 130, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1992.
  2. E. Bauer. Constitutive Modelling of Critical States in Hypoplasticity. Proceedings of the Fifth International Symposium on Numerical Models in Geomechanics, NUMOG V, Davos, Switzerland, Balkema, 15-20, 1995.
  3. E. Bauer. Calibration of a comprehensive hypoplastic model for granular materials. Soils and Foundations, 36(1):13--26, 1996.
  4. E. Bauer. Calibration of a comprehensive hypoplastic model for granular materials. Soils and Foundations Vol. 36, No. 1, 13-26 , 1996.
  5. E. Bauer. An objective description of critical states in hypoplasticity. Int. Symposium on Deformation and Progressiv Failure in Geomechanics, IS-NAGOYA 97, Nagoya, Japan, 347-352, 1997.
  6. E. Bauer. The critical state concept in hypoplasticity. 9th Int. Conf. on Computer Methods and Advances in Geomechanics, IACMAG 97, Wuhan, China, Balkema press 1997, 691-696, 1997.
  7. E. Bauer. Analysis of shear band bifurcation with a hypoplastic model for a pressure and density sensitive granular material. Mechanics of Materials, 31, 597-609, 1999.
  8. E. Bauer. Modelling of the Pressure and Density Sensitive Behaviour of Sand within the Framework of Hypoplasticity. Task Quarterly, Gdansk, Poland, Vol. 4, No. 3, 367-387, 2000.
  9. E. Bauer. Conditions for embedding Casagrande's critical states into hypoplasticity. Mechanics of Cohesive-Frictional Materials, 5, 125-148, 2000.
  10. E. Bauer, I. Herle. Stationary states in hypoplasticity. In D. Kolymbas, editor, Constitutive Modelling of Granular Materials, pages 167-192, Horton, 2000. Springer.
  11. E. Bauer, W. Huang. Effect of initial anisotropy on shear banding in granular materials. Proc. of the 7th Int. Symposium on Numerical Models in Geomechanics, Graz, Austria, Balkema press 1999, 121-126, 1999.
  12. E. Bauer., W. Huang. The Dependence of Shear Banding on Pressure and Density in Hypoplasticity. 4th Int. Workshop on Localization and Bifurcation Theory for Soils and Rock, Gifu, Japan, Balkema, 81-90, 1997.
  13. E. Bauer, W. Huang. Numerical study of polar effects in shear zones. Proc. of the 7th Int. Symposium on Numerical Models in Geomechanics, Graz, Austria, Balkema press 1999, 133-138, 1999.
  14. E. Bauer, W. Huang. Numerical investigation of polar effects in a Cosserat material under shearing. Proc. of the Int. Workshop on Fracture Mechanics and Advanced Engineering Materials, Sydney, Australia, University of Sydney, 311-318, 1999.
  15. E. Bauer, W. Huang. Particle size effects on the interface behavior between a granular layer and rough-rigid boundary layers under shearing. Proc. of the 7th Int. Conference on Composites Enginerring (ICCE/7), ed. D. Hui, Denver, USA, 71-72, 2000.
  16. E. Bauer, W. Huang. Influence of boundary conditions on the location and evolution of polar effects in a hypoplastic Cosserat material. Proc. of the 4th Euromech - Solid Mechanics Conference, Metz, France, 121, 2000.
  17. E. Bauer, W. Huang. The Evolution of Strain Localisation in a Hypoplastic Cosserat Material under Shearing. Task Quarterly, Gdansk, Poland, Vol. 4, No. 3, 469-483, 2000.
  18. E. Bauer, W. Hunag. Numerical investigation of strain localization in a hypoplastic Cosserat material under shearing. 10th Int. Conference on Computer Methods and Advances in Geomechanics, IACMAG, ed. S. Desai, Tucson, Arizona, Balkema press 2001, 525-528, 2001.
  19. E. Bauer, W. Hunag. Influence of density and pressure on spontaneous shear band formations in granular materials. IUTAM Symposium on Theoretical and Numerical Methods in Continuum Mechanics of Pourous Materials, ed. W. Ehlers, Stuttgart 1999, Germany, Kluwer Academic Publishers press 2001, 245-250., 2001.
  20. E. Bauer, W. Huang. Evolution of micro-polar effects in a granular layer under large shearing. Proc. of the 8th Int. Conference on Composites Enginerring (ICCE/8), ed. D. Hui, Tenerife, Spain, 67-68, 2001.
  21. E. Bauer., W. Huang. Evolution of polar quantities in a granular Cosserat material under shearing. Proceedings of the 5th Int. Workshop on Bifurcation and Localisation in Geomechanics, eds. H.-B. Mühlhaus and E. Pasternak, Perth, Australia, 1999, A. Balkema press, 2001, 227-238, 2001.
  22. E. Bauer, J. Tejchman. Numerical Study of the Effect of Grain Rotations on Material Behavior in a Fault Zone. Second International Conference on Mechanics of Jointed and Faulted Rock, Wien, Austria, Balkema, 317-322, 1995.
  23. E. Bauer, J. Tejchman. Influence of density, pressure and mean grain diameter on shear band localization in granular materials. Proc. of the 3th Int. Conf. on Mechanics of Jointed and Faulted Rock, MJFR-3, Wien, Austria, Balkema press 1998, 151-156, 1998.
  24. E. Bauer, W. Wu. A hypoplastic model for granular soils under cyclic loading. In D. Kolymbas, editor, Modern Approaches to Plasticity, pages 247--258. Elsevier, 1993.
  25. E. Bauer, W. Wu. Extension of hypoplastic constitutive model with respect to cohesive powders. In Siriwardane and Zaman, editors, Computer Methods and Advances in Geomechanics, pages 531--536. 1994.
  26. E. Bauer, W. Wu. A hypoplastic constitutive model for cohesive powders. Powder Technology, 85:1--9, 1995.
  27. R. Cudmani. Anwendung der Hypoplastizität zur Interpretation von Drucksondierwiderständen in nichtbindigen Böden. Geotechnik, 19(4):266-273, 1996.
  28. R. Cudmani, V. A. Osinov. The cavity expansion problem for the interpretation of cone penetration and pressuremeter tests. Canadian Geotechnical Journal, 38:622-638, 2001.
  29. F. Dahlhaus. Stochastische Untersuchungen von Silobeanspruchungen. Schriftenreihe des Institutes fr Massibau und Baustofftechnologie der Universität Fridericiana Karlsruhe, Heft 25, 1995.
  30. H.J. Feise. Modellierung des mechanischen Verhaltens von Schüttgütern. Veröffentlichung 23, Dissertation, Mechanik-Zentrum der Technischen Universität Carolo-Wilhelmina in Braunschweig, 1996.
  31. H.J. Feise, J. Schwedes. Anwendung des hypoplastischen Stoffmodells auf kohäsive Schüttgüter in Silos: Belastung des Austragorgans. `Silos - Forschung und Praxis' Tagung 96 in Karlsruhe, 1996.
  32. W. Fellin. Ein erster Einblick in die Hypoplastizität. Österreichische Ingenieur- und Architektenzeitschrift, 144(11-12):434-436, 1999.
  33. W. Fellin. Hypoplastizität für Einsteiger. Bautechnik, 77(1):10-14, 2000.
  34. G. Gudehus. A comparison of some constitutive laws for soils under radially symmetric loading and unloading. Proc. 3th Int. Conf. Num. Meth. Geom., Aachen, ed. Balkema, 1979.
  35. G. Gudehus. Ein umfassendes Konzept zum Nachweis der Tragfähigkeit und der Gebrauchtauglichkeit in der Geotechnik. Geotechnik, 17(2):83--103, 1994.
  36. G. Gudehus. Attractors for granular storage and flow. In PARTEC '95, 333--345, Nürnberg, 1995.
  37. G. Gudehus. A comprehensive concept for non-saturated granular bodies. In E. Alonso and P. Delage, editors, 1st Int. Conf. on Unsaturated Soils, pages 725--737, Paris, 1995. A.A.Balkema.
  38. G. Gudehus. A comprehensive constitutive equation for granular materials. Soils and Foundations, 36(1):1--12, 1996.
  39. G. Gudehus. Constitutive relations for granulate-liquid mixtures with a pectic constituent. Mechanics of Materials, 22:93--103, 1996.
  40. G. Gudehus. Silo Problems from a Geotechnical Viewpoint. `Silos - Forschung und Praxis' Tagung 96 in Karlsruhe, 1996.
  41. G. Gudehus. Attractors, percolation thresholds and phase limits of granular soils. In Behringer and Jenkins, editors, Powders and Grains, pages 169-183. Balkema, 1997.
  42. G. Gudehus. Shear localization in simple grain skeletons with polar effects. In Proc. 4th Int. Workshop on Localization and Bifurcation Theory for Soils and Rocks. Balkema, 1998.
  43. G. Gudehus, D. Kolymbas. A constitutive law of the rate type soils. 3th Int. Conf. Num. Meth. Geomech., Aachen, ed. Balkema 1979
  44. G. Gudehus, D. Kolymbas. Numerical testing of constitutive relations for soils. Proc. 5th Int. Conf. Num. Meth. Geomech., Nagoya, 1985.
  45. G. Gudehus, V. Mikulitsch. Materialverhalten zementierter Korngerüste. Bauingenieur, 71(2):119--126, 1996.
  46. I. Herle. Hypoplastizität und Granulometrie von Korngerüsten. In Vorbereitung, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1997.
  47. I. Herle. A relation between parameters of a hypoplastic constitutive model and grain properties. In T. Adachi, F. Oka, and A. Yashima, editors, Proc. 4th Int. Worksho p on Localization and Bifurcation Theory for Soils and Rocks, pages 91-98, Gifu, 1998. Balkema.
  48. I. Herle. Granulometric limits of hypoplastic models. TASK Quarterly, 4(3):389-407, 2000.
  49. I. Herle. Influence of pressure level and stress amplitude on the compaction of granular soils. In D. Kolymbas and W. Fellin, editors, Compaction of Soils, Granulates and Powders, volume 3 of Advances in Geotechnical Engineering and Tunneling, pages 285-295, Innsbruck, 2000. A.A.Balkema.
  50. I. Herle. Influence of pressure level and stress amplitude on the compaction of granular soils. In D. Kolymbas and W. Fellin, editors, Compaction of Soils, Granulates and Powders, volume 3 of Advances in Geotechnical Engineering and Tunneling, pages 285-295, Innsbruck, 2000. A.A.Balkema.
  51. I. Herle, T. Doanh. Verification of a hypoplastic model with static liquefaction tests on Hostun RF sand. In M. Jamiolkowski, R. Lancellotta, and D. Lo Presti, editors, Proc. 2nd Int. Symp. on Pre-failure Deformation Characteristics of Geomaterials, volume 1, pages 525-532, Torino, 1999. A.A.Balkema.
  52. I. Herle, T. Doanh, W. Wu. Comparison of hypoplastic and elastoplastic modelling of undrained triaxial tests on loose sand. In D. Kolymbas, editor, Constitutive Modelling of Granular Materials, pages 333-351, Horton, 2000. Springer.
  53. I. Herle, G. Gudehus. Determination of parameters of a hypoplastic constitutive model from properties of grain assemblies. Mechanics of Cohesive-Frictional Materials, 4(5):461-486, 1999.
  54. I. Herle, D. Kolymbas. Mechanisches Verhalten von Silogütern. In J. Eibl and G. Gudehus, editors, Silobauwerke und ihre spezifischen Beanspruchungen, pages 105-128. Wiley-VCH, 2000.
  55. I. Herle, P.-M. Mayer. Verformungsberechnung einer Unterwasserbetonbaugrube auf der Grundlage hypoplastisch ermittelter Parameter des Berliner Sandes. Bautechnik, 76(1):34-48, 1999.
  56. I. Herle, K. Nübel. Hypoplastic description of the interface behaviour. In G. Pande, S. Pietruszczak, and H. Schweiger, editors, Int. Symp. o n Numerical Models in Geomechanics, NUMOG VII, pages 53-58, Graz, 1999. A.A.Balkema.
  57. W. Huang, E. Bauer. A micropolar hypoplastic model for granular materials and its FEM implementation. Proc. of the 1st Asian-Pacific Congress on Computational Mechanics (APCOM01), eds. S. Valliappan and N. Khalili, Sydney, Australia, Elsevier Science Ltd. press, 1135-1140, 2001.
  58. H.M. Hügel. Prognose von Bodenverformungen. Heft 136, Dissertation, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1995.
  59. D. Kolymbas. A rate-dependent constitutive equation for soils. Mech. Res. Comm., 4:367--372, 1977.
  60. D. Kolymbas. Ein nichtlineares viskoplastisches Stoffgesetz für Böden. Veröffentlichungen Heft 77, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1978.
  61. D. Kolymbas. Bifurcation analysis for sand samples with a non-linear constitutive equation. Ingenieur-Archiv, 50, 131--140, 1981
  62. D. Kolymbas. A constitutive law of the rate type for soils. Position, calibration and prediction. In: "`Constitutive Relations for Soils --- Results of the Int. Workshop"', Grenoble, Balkema, 1982
  63. D. Kolymbas. Anelastic Deformation of Porous Media. In Fundamentals of Transport Phenomena in Porous Materials, Martinus Nijhoff, Den Haag, 1982
  64. D. Kolymbas. A generalized hypoelastic constitutive law. In Proc. XI Int. Conf. Soil Mechanics and Foundation Engineering, volume 5, page 2626, San Francisco, 1985. Balkema.
  65. D. Kolymbas. A constitutive law of the rate type for soils and other granular materials. Num. Meth. in Geomechanics, Kosice, 1987.
  66. D. Kolymbas. A novel constitutive law for soils. Second Int. Conf. on Constitutive Laws For Engineering Materials: Theory and Applications, Tucson, Arizona, January 1987, Elsevier, 1987
  67. D. Kolymbas. Generalized hypoelastic constitutive equation: Predictions for hollow-cylinder and cube tests, Proc. of the Int. Workshop on Constitutive Equations for Granular Non-Cohesive Soils, Case University, 1987
  68. D. Kolymbas. Eine konstitutive Theorie für Böden und andere körnige Stoffe. Veröffentlichungen Heft 109, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1988.
  69. D. Kolymbas. Generalized hypoelastic constitutive equation. In Saada and Bianchini, editors, Constitutive Equations for Granular Non-Cohesive Soils, pages 349--366. Balkema, 1988.
  70. D. Kolymbas. Stress strain behaviour of granular media. Third International Conference on Bulk Materials, Storage, Handling and Transportation, Newcastle (NSW Australia), 27-29 June, 1989
  71. D. Kolymbas. Computer-aided design of constitutive laws. International Journal for Numerical and Analytical Methods in Geomechanics, 15, 593-604 (1991)
  72. D. Kolymbas. An outline of hypoplasticity. Archive of Applied Mechanics, 61:143--151, 1991.
  73. D. Kolymbas. Hypoplasticity as a constitutive framework for granular materials. In Siriwardane and Zaman, editors, Computer Methods and Advances in Geomechanics, pages 197--208. Balkema, 1994.
  74. D. Kolymbas. Introduction to hypoplasticity, Advances in Geotechnical Engineering and Tunnelling, volume 1, Balkema, 2000.
  75. D. Kolymbas, E. Bauer. Soft oedometer -- a new testing device and its application for the calibration of hypoplastic constitutive laws. Geotechnical Testing Journal, 16(2):263--270, 1993.
  76. D. Kolymbas, G. Gudehus. A constitutive law for sands and clays --- position, prediction and evaluation. In: Proc. of the Workshop on Limit Equilibrium, Plasticity and Generalized Stress-Strain in Geotechnical Engineering, Montreal, 1980. Published by ASCE, 1981
  77. D. Kolymbas, I. Herle, P.-A. v. Wolffersdorff. Hypoplastic constitutive equation with back stress. International Journal of Numerical and Analytical Methods in Geomechanics, 19(6):415--446, 1995.
  78. D. Kolymbas, I. Herle. Hypoplasticity: A framework to model granular materials. In B. Cambou, editor, Behaviour of granular materials. CISM courses and lectures No. 385, pages 239-268. Springer, 1998.
  79. D. Kolymbas, S.V. Lavrikof, A.F. Revuzhenko. Odnorodnoje Deformirovanije syputschej sredy. Teorija i experiment (Homogeneous deformation of granular media. Theory and experiment). Prikladnaya Mathematika i Technitscheskaya Fisika. (ISBN 0869-5032), 6, 1994, S. 114-121.
  80. D. Kolymbas, G. Rombach. Shear band formation in generalized hypoelasticity. Ingenieur-Archiv, 59, 177--186, 1989
  81. D. Kolymbas, M. Topolnicki. A generalization of Hvorslev's equivalent stress. In Swoboda, editor, Numerical Methods in Geomechanics, pages 321--326. Balkema, 1988.
  82. D. Kolymbas, W. Wu. Recent results of triaxial test with granular materials. Silos - Forschung und Praxis, Tagung '88. Tagungsband, herausgeg. Sonderforschungsbereich 219 `Silobauwerke und ihre spezifischen Beanspruchungen', Universität Karlsruhe, 99-117, 1988.
  83. D. Kolymbas, W. Wu. Recent results of triaxial test with granular materials. Powder Technology, 60, 99--119, 1990
  84. D. Kolymbas, W. Wu. Introduction to hypoplasticity. In D. Kolymbas, editor, Modern Approaches to Plasticity, 213-223. Elsevier, 1993.
  85. P. Kudella. Stabilitätsberechnung von setzungsgefährdeten Kipprandböschungen. Geotechnik, 19, Heft 1, 7-15, 1995.
  86. C. Lyle. Spannungsfelder in Silos mit starren, koaxialen Einbauten. Diss., Fakultät für Maschinenbau und Elektrotechnik der TU Carolo-Wilhelmina zu Braunschweig, 1993.
  87. A. Niemunis. Hypoplasticity vs. elastoplasticity, selected topics. In D. Kolymbas, editor, Modern Approaches to Plasticity, pages 278--307. Elsevier, 1993.
  88. A. Niemunis. A visco-plastic model for clay and its fe implementation. In E. Dembicki, W. Cichy, and L. Balachowski, editors, Recent results in mechanics of soils and rocks., pages 151-162. TU Gdansk, 1996.
  89. A. Niemunis, I. Herle. Hypoplastic model for cohesionless soils with elastic strain range. Mechanics of Cohesive-Frictional Materials, 2(4):279-299, 1997.
  90. K. Nübel, R. Cudmani. Examples of finite element calculations with the hypoplastic law. In D. Kolymbas, editor, Constitutive Modelling of Granular Materials, pages 523-538. Springer, 2000.
  91. K. Nübel, C. Karcher. FE simulations of granular material with a given frequency distribution of voids as initial condition. Granular Matter, 1:105-112, 1998.
  92. K. Nübel, C. Karcher, I. Herle. Ein einfaches Konzept zur Abschätzung von Setzungen. Geotechnik, 22(4):251-258, 1999.
  93. V. Osinov, R. Cudmani. Theoretical investigation of the cavity expansion problem based on a hypoplasticity model., 2001.
  94. V. A. Osinov. Theoretical investigation of large-amplitude waves in granular soils. Soil Dynamics and Earthquake Engineering, 17:13-28, 1998.
  95. V. A. Osinov, G. Gudehus. Plane shear waves and loss of stability in a saturated granular body. Mechanics of Cohesive-Frictional Materials, 1(1):25-44, 1996.
  96. V.R. Raju. Spontane Verflüssigung lockerer granularer Körper - Phänomene, Ursachen, Vermeidung. Heft 134, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1994.
  97. G.A. Rombach. Schüttguteinwirkungen auf Silozellen, Exzentrische Entleerung. Veröffentlichungen Heft 14, Dissertation, Institut für Massivbau und Baustofftechnologie der Universität Fridericiana in Karlsruhe, 1991.
  98. C. Ruckenbrod. Statische und dynamische Phänomene bei der Entleerung von Silozellen. Schriftenreihe des Institutes für Massivbau und Baustofftechnologie der Universität Fridericiana in Karlsruhe, Heft 26, 1995.
  99. Z. Sikora. Hypoplastic flow of granular materials. A numerical approach. Veröffentlichungen Heft 123, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1992.
  100. Z. Sikora, W. Wu. Shear band formation in beaxial tests. Proc. Int. Conf. on Constitutive Laws for Engineering Materials, Tucson, Arisona, USA, 1991.
  101. C. Tamagnini, G. Viggiani, R. Chambon. A review of two different approaches to hypoplasticity. In D. Kolymbas, editor, Constitutive modelling of granular materials, pages 107-145. Springer, 2000.
  102. C. Tamagnini, G. Viggiani, R. Chambon, J. Desrues. Evaluation of different strategies for the integration of hypoplastic constitutive equations. Application to the CLoE model. Mechanics of Cohesive-Frictional Materials, 5, 2000.
  103. J. Tejchman, E. Bauer. Numerical simulation of shear band formation with a polar hypoplastic constitutive model. Computers and Geotechnics, Vol. 19, No. 3, 221-244, 1996.
  104. J. Tejchman, I. Herle. A ''class A'' prediction of the bearing capacity of plane strain footings on sand. Soils and Foundations, 39(5):47-60, 1999.
  105. J. Tejchman, I. Herle, W. Wehr. FE studies on the influence of initial void ratio, pressure level and mean grain diameter on shear localisation. International Journal for Numerical and Analytical Methods in Geomechanics, 23(15):2045-2074, 1999.
  106. J. Tejchman, W. Wu. Numerical simulation of shear band formation with a hypoplastic constitutive model. Computers and Geotechnics, 18(1):71--84, 1996.
  107. M. Topolnicki. Observed stress-strain behaviour of remoulded saturated clay and examination of two constituive models. Heft 107, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1987.
  108. W. Wehr, I. Herle, G. Gudehus. Sand anchors - simulations with a Couette device. In T. Adachi, F. Oka, and A. Yashima, editors, Proc. 4th Int. Worksho p on Localization and Bifurcation Theory for Soils and Rocks, pages 189-198, Gifu, 1998. A.A.Balkema.
  109. W. Wehr, J. Tejchman, I. Herle, G. Gudehus. Sand anchors - a shear zone problem. In A. Asaoka, T. Adachi, and F. Oka, editors, IS-Nagoya'97: Deformation and Progressive Failure in Geomechanics, pages 787-792. Pergamon, 1997.
  110. P.-A. von Wolffersdorff. A hypoplastic relation for granular materials with a predefined limit state surface. Mechanics of Cohesive-Frictional Materials, 1:251--271, 1996.
  111. P.-A. von Wolffersdorff. Verformungsprognosen für Stützkonstruktionen. In Vorbereitung, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1997.
  112. J. Weidner. Überprüfung der Verbesserung eines Stoffansatzes für ruhende und schnell flie Schüttgüter. Silos - Forschung und Praxis, Tagung '88. Tagungsband, herausgeg. Sonderforschungsbereich 219 `Silobauwerke und ihre spezifischen Beanspruchungen', Universität Karlsruhe, 88-98, 1988.
  113. J. Weidner. Vergleich von Stoffgesetzen granularer Schüttgüter zur Silodruckermittlung. Veröffentlichungen Heft 10, Dissertation, Institut für Massivbau und Baustofftechnologie der Universität Fridericiana in Karlsruhe, 1990.
  114. W. Wu. Hypoplastizität als mathematisches Modell zum mechanischen Verhalten granularer Stoffe. Veröffentlichungen Heft 129, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1992.
  115. W. Wu. Rational approach to anisotropy of sand. International Journal for Numerical and Analytical Methods in Geomechanics, 22:921-940, 1998.
  116. W. Wu. On a simple critical state model for sand, Proc. International Symposium on Numerical Methods in Geomechanics, Graz, Austria, pp. 47-52, Balkema, 1999
  117. W. Wu. Nonlinear analysis of shear band formation in sand, International Journal for Numerical and Analytical Methods in Geomechanics, 24, 245-263, 2000
  118. W. Wu, E. Bauer. A hypoplastic model for barotropy and pyknotropy of granular soils. In D. Kolymbas, editor, Modern Approaches to Plasticity, 225-245. Elsevier, 1993.
  119. W. Wu, E. Bauer. A simple hypoplastic constitutive model for sand. International Journal of Numerical and Analytical Methods in Geomechanics, 18:833--862, 1994.
  120. W. Wu, E. Bauer, D. Kolymbas. Hypoplastic constitutive model with critical state for granuar materials. Mechanics of Materials, 23:45--69, 1996.
  121. Wu, W. and Bauer, E., A hypoplastic constitutive model for barotropy and pyknotropy of granular soils, Proc. Int. Workshop on Modern Approaches in Plasticity, Kolymbas editor, Horton, Greece, pp. 225 - 245, Elsevier, 1992
  122. W. Wu, E. Bauer, A. Niemunis, I. Herle. Visco-hypoplastic models for cohesive soils. In D. Kolymbas, editor, Modern Approaches to Plasticity, 365-383. Elsevier, 1993.
  123. W. Wu, W. Hunag. Rational approach to anisotropy of rocks, Proc. EUROCK Symposium, 27.-31.März, 2000, Aachen , pp. 623-628, Verlag Glückauf
  124. W. Wu, D. Kolymbas. Numerical testing of the stability criterion for hypoplastic constitutive equations. Mechanics of Materials, 9:245--253, 1990.
  125. W. Wu, D. Kolymbas. Hypoplasticity, then and now, in: Constitutive Modelling of Granular Materials, Kolymbas editor, Springer Verlag, 2000
  126. W. Wu, A. Niemunis. Beyond invertibility surface in granular materials. In Chambon, Desrues, and Vardoulakis, editors, Localisation and Bifurcation Theory for Soils and Rocks, 113--126. Balkema, 1994.
  127. W. Wu, A. Niemunis. Failure criterion, flow rule and dissipation function derived from hypoplasticity. Mechanics of Cohesive-Frictional Materials, 1:145--163, 1996.
  128. W. Wu, A. Niemunis. Beyond Failure in Granular Materials. Int. J. for Numerical and Analytical Methods in Geomechanics,21, 153-174, 1997
  129. W. Wu, Z. Sikora. Localized bifurcation in hypoplasticity. International Journal of Engineering Science, 29(2):195--201, 1991.
  130. W. Wu, Z. Sikora. Localized Bifurcation of Pressure Sensitive Dilatant Granular Materials. Mechanics Research Communications, Vol. 29, 289-299, 1992.
  131. Wu, W., Tejchman, J. and Bauer, E., Numerical simulation of progressive failure in soils, Proc. Int. Conf. on Numerical Methods in Stuctural & Geotechnical Engineering, Hongkong, pp. 819-823, 1994
  132. S.-A. Zaimi, J.-B. Guillot, C. Petit, J.-M. Steiler. Modelling the flow of solids in the blast furnace. In Iron and Steel Making. Toronto, 1998.
  133. M. Ziegler. Berechnung des verschiebungsabhängigen Erddrucks in Sand. Veröffentlichungen Heft 101, Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, 1986.

References on Barodesy

Finite Element implementation of hypoplasticity

You can download our implementations for sand hypoplasticity in the basic version (von Wolffersdorff, 1996) and for hypoplasticity with small strain stiffness (Niemunis and Herle, 1997)  from soilmodels.com.

Element test simulations, Test data, ...

soilmodels.com: free implementations

Nach oben scrollen