Who has never played with soap bubbles as a kid? Blowing into a ring-shaped object filled with soap liquid creates bubbles whose membranes consist in a thin soap film, and the game consists in observing their movements, deformations, whether we can merge them together, or burst them. The phenomenon that enables a soap bubble to be what it is, namely a cohesive structure that encloses a volume, is called surface tension. These entertaining soap bubbles actually hide physical phenomena that have much more serious implications, in particular in industrial processes like paint production, design of food products, or medical treatments. This phenomenon is also central for light-weight insects that locomote on the surface of swamps. Therefore stability questions related to surface tension phenomena are of crucial importance.
What is surface tension?
At the molecular level, water molecules are organized, in some sense, in order to stick to each other inside the liquid, and the resulting net force is basically zero. But at the surface, at the interface with another medium like air for example, these molecules are organized differently due to the cohesive forces that are inequal at the contact with air. At the macroscopic level, they then form a curved interface which induces a difference of pressure between both sides, and the resulting force is the so-called surface tension force. This macroscopic force is proportional to the mean curvature of the interface. More generally, the term surface tension refers to the tendency of liquid molecules to create cohesive forces in reaction to differences of densities, viscosities or pressure between two fluids (gas, liquid, etc...).
When do soap bubbles burst?
The cohesive forces that maintain this thin interface can possibly break. When does this happen? Well, it basically depends on several parameters: The viscosities of the fluids, the inertial forces (related to the densities) that intervene, and the magnitude of the surface tension, represented by a coefficient. For example, the small bubbles that we observe in our bath, the globules that circulate in our blood vessels, or the rain drops on plant leaves barely burst. This is due to the fact that, at this scale, the inertial forces (like gravity for example) are negligible. When the inertial forces rather play a significant role, bouncing effects are possible, and the Kolmogorov theory predicts that the soap bubble bursts when its maximal diameter reaches a critical value, expressed as a power of the ratio between the inertial forces and the surface tension forces. The exponent of this power, leading to the expression of this critical diameter, has been experimentally determined and validated in [Hin55].
Surfaces of minimal energy
When the soap bubble does not burst, and when no external force is exerted, the volume enclosed by the soap bubble remains constant, since the fluid inside is generally incompressible. But the surface occupied by the soap bubble can vary, and tends asymptotically to a surface of minimal energy. What do we mean by energy? There are roughly two types of energies: the kinetic energy, induced by the velocity and density of fluid particles inside and outside the soap bubble, and the potential energy, which is, in our context, proportional to the area of the surface that constitutes the soap bubble. Both energies are dissipated by the viscosity forces, and thus, at the equilibrium, when the particles of the whole system are immobile, the kinetic energy is reduced to zero, and the configuration corresponds to an immobile surface of minimal area. What is this surface? Without contact with any outer boundary or other structure, this surface is nothing else than a sphere. There are several ways of proving this result mathematically, either by showing for example that it corresponds to a surface of constant mean curvature, or by exploiting the notion of symmetry. The time convergence to the equilibrium is illustrated in Figures 1 and 2. Further details and illustrations are presented in [SC19]. At the equilibrium, the radius \(R\) of the soap bubble is related to the difference between the outside pressure \(p^+\) and the inside pressure \(p^-\) via the so-called Young-Laplace equation:
\begin{equation} \tag{$\ast$} p^+ - p^- = \displaystyle -\frac{\mu}{R}, \label{Young} \end{equation}
where \(\mu > 0\) denotes the surface tension coefficient. Note that this formula shows in particular that the pressure is larger inside than outside the soap bubble.
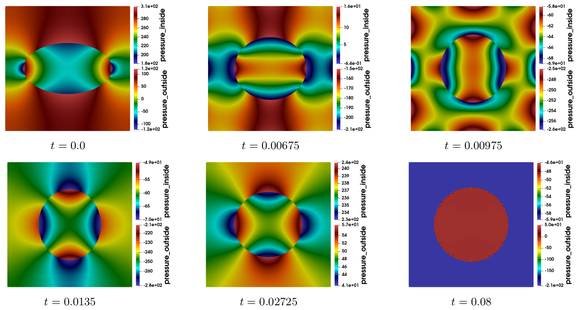
Figure 1: Time evolution of the pressure fields on both sides of a bouncing soap bubble, which converges ultimately to a circle. The difference between the asymptotic pressures satisfies equation (∗).
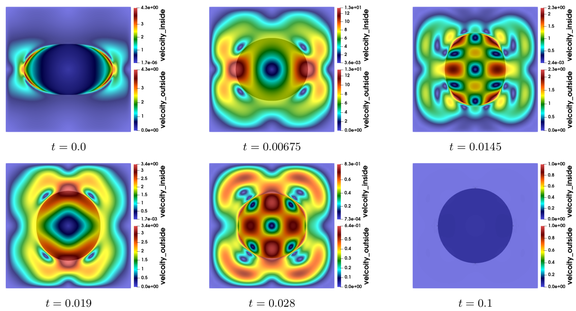
Figure 2: Time evolution of the magnitude of the velcoity fields on both sides of a bouncing soap bubble, which converges ultimately to a circle. The equality of velocities holds at the interface.
Control and stabilization of soap bubbles and liquid drops
The goal is to ensure that the soap bubble never bursts. Instead of trying to keep its inertial forces small enough, or its deformation not too large, one can rather design additional forces, exerted on the interface, in order to control its dynamics towards an equilibrium state. These additional forces can be exerted via the use of a surface active agent (a chemical compound succintly called surfactant) possibly combined with an electric field, for example. Further, the way these forces are applied can also be designed in a feedback loop, such that the controlled system is fully stabilized, and prevents large deformations of the soap bubble that could lead to its breakup. The theoretical investigations in this direction have been rigorously developed in two works published recently, namely [SC23, SC24]. The methods employed in these articles for that purpose pave the way to actual realizations of these control forces, and are expected to be extended in the near future to numerical illustrations and more complex related problems.
References
[Hin55] Hinze, J. (1955). Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE Journal, 1:289-295, 1955.
[SC19] Court, S. (2019). A fictitious domain approach for a mixed finite element method solving the two-phase Stokes problem with surface tension forces. J. Comput. Appl. Math. 359:30-54, 2019.
[SC23] Court, S. (2023). Approximate controllabillity of a 2D linear system related to the motion of two fluids with surface tension. Proceedings in Applied Mathematics and Mechanics, 23, e202300083, 2023.
[SC24] Court, S. (2024). Feedback Stabilization of a Two-Fluid Surface Tension System Modeling the Motion of a Soap Bubble at Low Reynolds Number: The Two-Dimensional Case. J. Math. Fluid Mech. 26, 7, 2024.
This work is licensed under a Creative Commons Attribution 4.0 International License.
Written by Sébastien Court in February 2024
Assistant Professor at DiSC & Department of Mathematics
University of Innsbruck
About the author
My background are numerical simulations of fluid-structure interactions, elasticity theory, scientific computing, and optimal control theory. At the Digital Science Center, I work on the mathematical foundations of Deep Learning.
Research Area
Artificial Neural Networks, Mathematical Optimization, and Dynamical Systems



