Roland HINTERHÖLZL
Modellierung des zeitabhängigen Verhaltens von faser- und partikel- verstärkten· Verbundwerkstoffen mit Hilfe der Viskoelastizitätstheorie und der Schädigungsmechanik
2001
1 Abstract
Reinforced plastics show a strong time dependent behavior that is introduced by the time dependent behavior of the matrix whereas the reinforcing fibers or particles are usually time independent, see fig. 1. The aim is to model this behavior by the theory of viscoelasticity and non-linear effects within the theory of continuum damage mechanics.
Studied are fiber reinforced plastics reinforced by swirl-mat used as plates and reinforced by cut fibers used as pipes. Here the long time behavior is modeled (e.g. creep till failure). The particulate composites investigated are solid propellant and asphalt concrete where the influence of the loading rate is modeled, see fig.2. Constitutive equations are developed and proposed, to be implemented in the FEM program ABAQUS. The FEM results are compared to analytical and experimental results.
| A | B |
|---|---|
| Fig. 1: Change of the vertical diameter of a GRP Pipe, under a constant vertical load applied at the top, versus time | Fig. 2: Schematical stress-strain curves·for uniaxial tension tests of a particulate composite, e.g. solid propellant, under 2 different loading (displacement) rates |
2 Results
2.1 Linear Viscoelastic Models
An orthotropic viscoelastic constitutive law is implemented in ABAQUS and verified by analytical example (to predict the response of a long thick-walled cylindrically anisotropic cylinder that is subjected to an internal pressure p=P*H(t) with H(t) as the Heaviside step function is investigated). The results agree very well, see fig. 3.
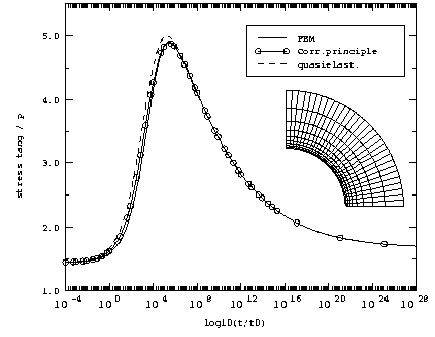
Fig. 3: Tangential stress at the inner surface of the cylinder versus time for the FEM solution and the analytical solutions according to the correspondence principle and the quasielastic method, and the FEM mesh
2.2 Nonlinear Viscoelastic Models - Viscoelasticity-Damage Models
Modeling the longtime behavior up to failure of a swirl mat composite
Some of the layers used in the GFRP pipes under consideration can be compared to swirl-mat composites. The damage is mainly constricted to randomly distributed matrix-cracks. It is assumed that the virgin material symmetry remains unchanged by the ensuing damage pattern. The following assumptions are made: phenomenological isotropic damage model, no damage induced anisotropy, uncoupled volumetric and deviatoric response, small strains, and proportional loading (one step creep loading). Thus, the constitutive equations of an isotropic viscoelasticity/damage model with a single damage variable y follow. For verification we investigate an uniaxial creep test of a swirl-mat composite for which an analytical solution for e(t) based on a coupled viscoelastic/damage model was proposed by Tawab and Weitsman 1998.
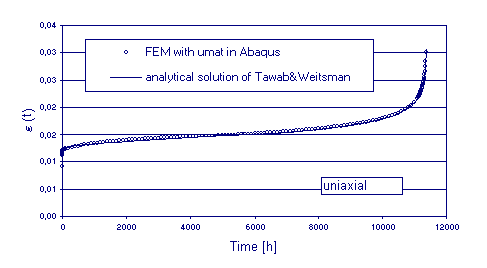
Fig. 4: FEM results compared to analytical results for a uniaxial creep test of a swirl mat Composite
Modeling the loading rate dependence of short time tests of particulate composites
Asphalt concrete and solid propellant are both particulate composites containing particles that can be assumed as rigid. Thus just a single creep function is needed to characterize the linear viscoelastic behavior. For a viscoelastic material with general three dimensional loading and with growing damage, always three principal strains and their directions can be obtained. The basic underlying assumption is that with the distributed damage dominated by opening-mode microcracks on the planes perpendicular to the maximum principal direction of the strain, the composite body is transversely isotropic with the axis of symmetry oriented in the current maximum principal strain direction. We also assume that the composite is isotropic in the absence of damage. It is further assumed that the composite is linearly elastic or viscoelastic for a fixed amount of damage. For a composite with this type of oriented damage, the principal axes of stress and strain are aligned. For verification a biaxial experiment of Ha and Schapery 1998 is chosen: a finite strip with a center hole and an I-shape thickness. The top of the strip is pulled with a defined displacement rate. The FEM-results for the global load versus the global strain, that is defined as the global displacement divided by the height of the specimen, are compared to the results of two tests, H1 and H3, in fig. 5. The FEM-results fit the test data very well. Furthermore localization and mesh dependence are studied and the by digital image correlation (DICM) investigated full field surface strains in the stressed filled rubber structures are compared to the calculated strain fields, but not shown here.
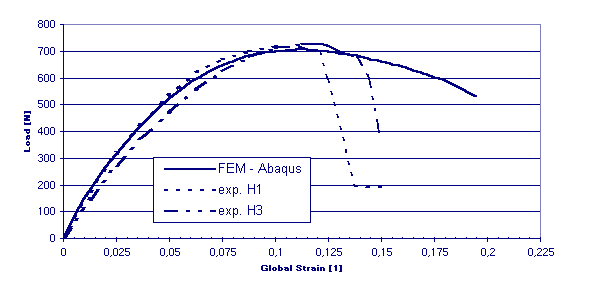
Fig. 5: FEM results compared to experimental results - Load vs Global Strain, for solid propellant
2.3 Temperature Effects
Two kinds of temperature effects have to be considered: thermal expansion and the effect of temperature on the linear viscoelastic behavior. As long as the coefficient of thermal expansion, aT, varies with temperature but is independent of the temperature history and independent of damage the thermal expansion can be treated within the framework provided by ABAQUS. The temperature effects on the viscoelastic behavior can be treated for thermorheological simple materials within the theory of the Time-Temperature-Superposition-Principle (TTSP) by introducing a reduced time, for theoretical background see e.g. Ferry 1980. This feature is included in all the implementations done into ABAQUS within this work.
2.4 Future Goals
For the particle reinforced plastics the experimental and numerical results agree very well. The model, in its present form, can only predict material response up to, or perhaps slightly beyond, the peak of the stress-strain response. When a macrocrack develops (usually somewhere after the peak load) one may switch to a fracture mechanics approach for modeling the remaining response to failure. A more integrated approach that could model the entire response range would be preferable; this is potentially possible if the damage localization associated with post peak behavior can be correctly captured in a numerical approach. For modelling the fibre reinforced plastics the comparison between numerical and analytical results fit very well. In future more experiments should be conducted for verification.
3 Conclusions
Constitutive equations for orthotropic linear viscoelastic materials, and for viscoelastic materials with growing damage in the FEM were derived and implemented. Long time behavior in form of secondary and tertiary creep could be modeled as well as short time behavior in form of the response to different loading rates. The numerical results fitted very well with the analytical and experimental data. The viscoelasticity/damage equations could be applied successfully to fiber reinforced as well as particulate composites. This is a step in the modeling of the time-dependent behavior of composites. In the long run the aim is to make such complex constitutive models available and "usable" for more engineers, and especially not just for research but also for the design of structures.
