Matthias HOFMANN
Integrationsalgorithmen und Parameteridentifikation elasto-plastischer Stoffgesetze für teilgesättigte Materialien
2010
- Kurzfassung auf Deutsch
Abstract
The integration of elasto-plastic constitutive models for determining the stresses is an important part of nonlinear finite element analyses. This thesis deals with the stress update of elasto-plastic material models for partially saturated materials (cf. figure). Taking partially saturated conditions into account yields complex constitutive models. In the last two decades a number of material models for partially saturated soils have been proposed. The Barcelona Basic Model (BBM) (Alonso et al.,1990), a cap model for partially saturated soils (Kohler, 2006) and an extension of these models for modelling of swelling soils, described by Sanchez et al. (2005), are investigated in this work.
Integration algorithms reported in the literature are adapted for the stress update of unsaturated soil models. Explicit and semi-explicit methods are applied in addition to the popular return mapping algorithm. Additionally, an implicit integration scheme, formulated in terms of stress invariants, is developed, furthermore the Richardson extrapolation is applied to all of these methods for error control. Moreover a fifth-order Runge-Kutta stress update algorithm with error control is included in the investigations. In addition to reliability, robustness and accuracy the effciency is a desired feature of stress integration algorithms. As shown in this thesis the computing time of the return mapping algorithm can be reduced substantially with the developed integration methods.
A large number of constitutive parameters, e.g. 11 parameters in the case of the BBM, are required for unsaturated soil models. Not all of them have a physical meaning and, hence, they cannot be determined from experiments directly. Thus, parameter identification by means of optimization methods is of special importance. In this work the parameters are identified by minimizing an objective function. Since this optimization problem has many local minima, in this work a global optimization algorithm, the particle swarm method, is applied.
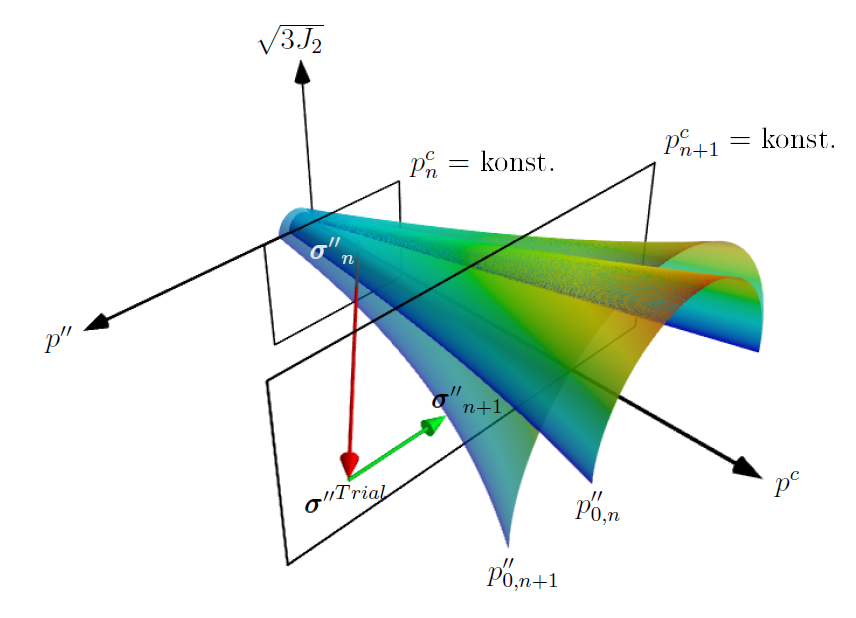
Fließflächen des Barcelona Basic Modells für zwei unterschiedliche Werte der Kapillarspannung
Die Integration elasto-plastischer Stoffgesetze zur Ermittlung der Spannungen ist ein wichtiger Teil nichtlinearer Berechnungen mit der Methode der finiten Elemente. Diese Arbeit behandelt die Spannungsberechnung elasto-plastischer Materialmodelle für teilgesättigte Materialien.
Durch die Berücksichtigung teilgesättigter Zustände entstehen komplexe Stoffgesetze. In den letzten beiden Jahrzehnten wurden einige Materialmodelle zur Beschreibung teilgesättigter Böden vorgeschlagen (siehe Abbildung). In dieser Dissertation werden das Barcelona-Basic-Modell (BBM) (Alonso et al., 1990), ein für teilgesättigte Zustände erweitertes Kappenmodell (Kohler, 2006) und die von Sanchez et al. (2005) beschriebene Möglichkeit, diese Modelle zur Modellierung von quellfähigen Böden zu erweitern, untersucht.
In der Literatur beschriebene Integrationsalgorithmen werden zur Spannungsberechnung teilgesättigter Böden angepasst und miteinander verglichen. Neben dem (am weitesten verbreiteten) allgemeinen Projektionsverfahren werden explizite und halb-explizite Methoden verwendet. Darüberhinaus wird ein in Spannungsinvarianten formuliertes implizites Integrationsschema entwickelt. Diese Verfahren werden mit der Richardson-Extrapolation kombiniert, um eine Fehlerkontrolle zu erhalten. Zum Vergleich und zur Berechnung sehr genauer Lösungen wird der Radau5-Algorithmus verwendet. Neben der Robustheit und Genauigkeit der Integrationsverfahren spielt deren Effzienz eine wesentliche Rolle. Mit den in dieser Dissertation entwickelten Integrationsmethoden kann bei gleicher Genauigkeit die Rechenzeit des allgemeinen Projektionsverfahrens deutlich reduziert werden.
Die meisten elasto-plastischen Materialmodelle für teilgesättigte Böden benötigen eine große Anzahl von Materialparametern, z.B. 11 Parameter im Fall des BBM. Nicht alle weisen eine physikalische Bedeutung auf und sind daher nicht direkt aus Versuchen bestimmbar. Aus diesem Grund ist die Parameteridentifikation mit Hilfe eines Optimierungsverfahrens wichtig. In dieser Arbeit werden die Parameter durch Minimierung einer Zielfunktion ermittelt. Da dieses Optimierungsproblem mehrere lokale Minima aufweist, wird diese Aufgabe mit einem globalen Optmierungsverfahren, der Partikel-Schwarm-Methode, gelöst.
