KnitEuler Moria SCHWARZ (Master Thesis)
This thesis engages in an interdisciplinary investigation that bridges the art of knitting and the mathematical principles of graph theory. The main inspiration comes from the inherent principle of reusability that characterizes the craft of knitting, an aspect that the project aims to exploit and apply to architectural and structural patterns.
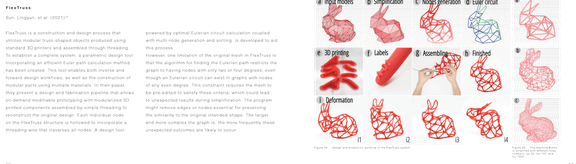
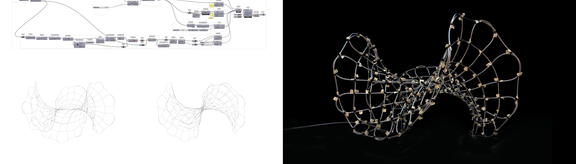
Knitting uses a single continuous thread to form a series of patterns and designs. This feature allows for sustainable use due to its unique property of reusability. An entire knitted piece can be methodically disassembled by pulling on one end, returning the yarn to its original state, allowing it to be reused. By applying this fundamental property of knitting to the design of structures, that follows specific logics of Eulerian paths. the research proposes the development of a dynamic system based on the use of a single thin, continuous, and flexible element.
Exploring the void between monolithic and discrete structures, in order to determine the assembly process, a range of algorithms rooted in graph theory are utilized, particularly those developed for identifying Euler paths. These algorithms specialize in identifying paths that traverse all edges of a graph exactly once and modifying a new approach that takes into account the physical aspects unique to the system under study. What emerges from this design approach and inherent methodology is a speculative spatial expression, driven by patterns, pathlogics, and material properties.