Cavity Quantum Electrodynamics
Cavity Quantum E-Dyn.
Helmut Ritsch's Theory Group | Universität Innsbruck
CQED Theory
Helmut Ritsch

Research
This page details our research efforts and interests. Below you will find a selection of topics we are currently working on. For a list of publications please see the links.
General research statement
Our research covers the fields of theoretical quantum optics and ultra cold gas physics with strong connections to quantum information theory, foundations of quantum physics and quantum theory of condensed matter systems. We focus on full quantum descriptions of matter and light waves, which are strongly coupled by momentum exchange. Our aim is an effective theoretical description of real physical systems in a close connection with experiments, where genuine quantum phenomena as quantum phase transitions, entanglement and macroscopic super positions can be studied in a well-controlled and understood environment.
Publications
For an (almost) complete list of publications that have emerged from our research, please visit
or contact us directly.
Light forces in high-Q cavities
Cavity cooling
Freezing particles in very small regions in space is the prerequisite for any investigation (like spectroscopy) or manipulation (like quantum computation). As photons carry energy and momentum, absorption, emission, and coherent scattering of light creates forces on the involved particles. For light enclosed between two highly reflective mirrors, i.e. an optical resonator, these forces are strongly enhanced. They can be tailored to control the quantum motion of the particles. This allows for trapping atoms and molecules as well as cooling them to temperatures very close to the absolute zero.
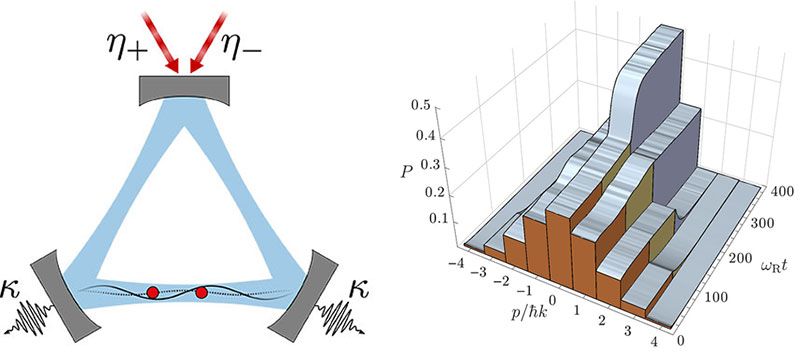
Collective effects of atoms with light-induced interactions
Self-organization
Photons carry momentum and their scattering thus not only modifies light propagation but induces forces on particles. Hence, coupling mobile scatterers to the modes of nonlinear optical devices such as optical resonators or optical nano-fibers generates complex coupled nonlinear dynamics. The induced long-range dipole-dipole interactions and collective scattering induces a phase transition from random order to a crystalline structure for illumination at sufficient power. This minimizes the optical potential energy of the particles in concurrence with a maximization of light scattering into the resonator. Such adaptive self-ordering dynamics in optical resonators can be implemented in a wide range of systems from cold atoms and molecules to mobile nanoparticles in solution.
In the quantum regime ultracold atoms in resonators establish a promising platform for investigating emergent phases of complex quantum matter in a well-controlled environment. This enables the exploration of intriguing many-body effects such as Dicke superradiance, supersolidity, spontaneous quasi-crystallization and spin self-ordering.
Since the first experimental demonstration of atomic self-ordering in a system composed of a Bose-Einstein condensate coupled to a quantized electromagnetic mode of a high-Q optical cavity, the field has rapidly evolved over the past decade. Recent developments and the current status in the field of quantum-gas cavity QED are described pedagogically in our extensive review article.
- F. Mivehvar, F. Piazza, T. Donner, and H. Ritsch: arXiv:2102.04473 (2021)
- S. Ostermann, F. Piazza and H. Ritsch: Phys. Rev. X 6, 021026 (2016)
- F. Mivehvar, H. Ritsch and F. Piazza: Phys. Rev. Lett. 122, 113603 (2019)
- E. Colella, S. Ostermann, W. Niedenzu, F. Mivehvar and H. Ritsch: New J. Phys. 21, 043019 (2019)
- D. Holzmann and H. Ritsch: New J. Phys. 18 103041 (2016)
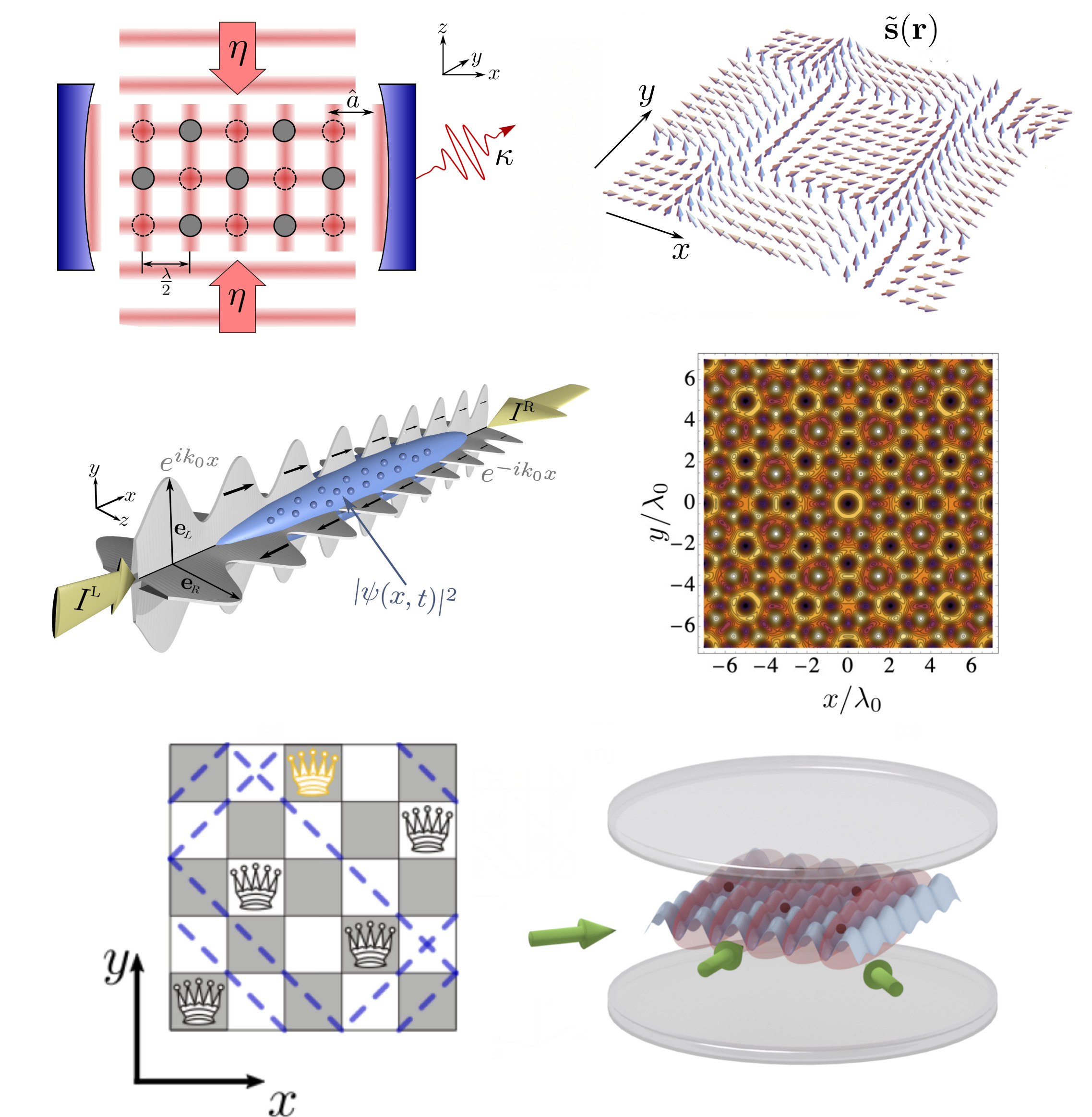
Quantum optimization
The self-consistent optimization of cavity field and atomic distribution due to the non-linear interaction establishes a nice tool for the solution of specific quantum optimization problems with atoms in resonators. For example, as we showed recently, ultracold atoms in an optical lattice with cavity-mediated long-range interactions constitute a quantum simulator for the excluded diagonals N-queens completion problem. If several illumination colors and cavity modes are applied, particles adapt to various illumination conditions dynamically to ensure maximal simultaneous scattering of all frequencies. This constitutes a system with a built-in memory to simulate Hopfield networks and associative memories.
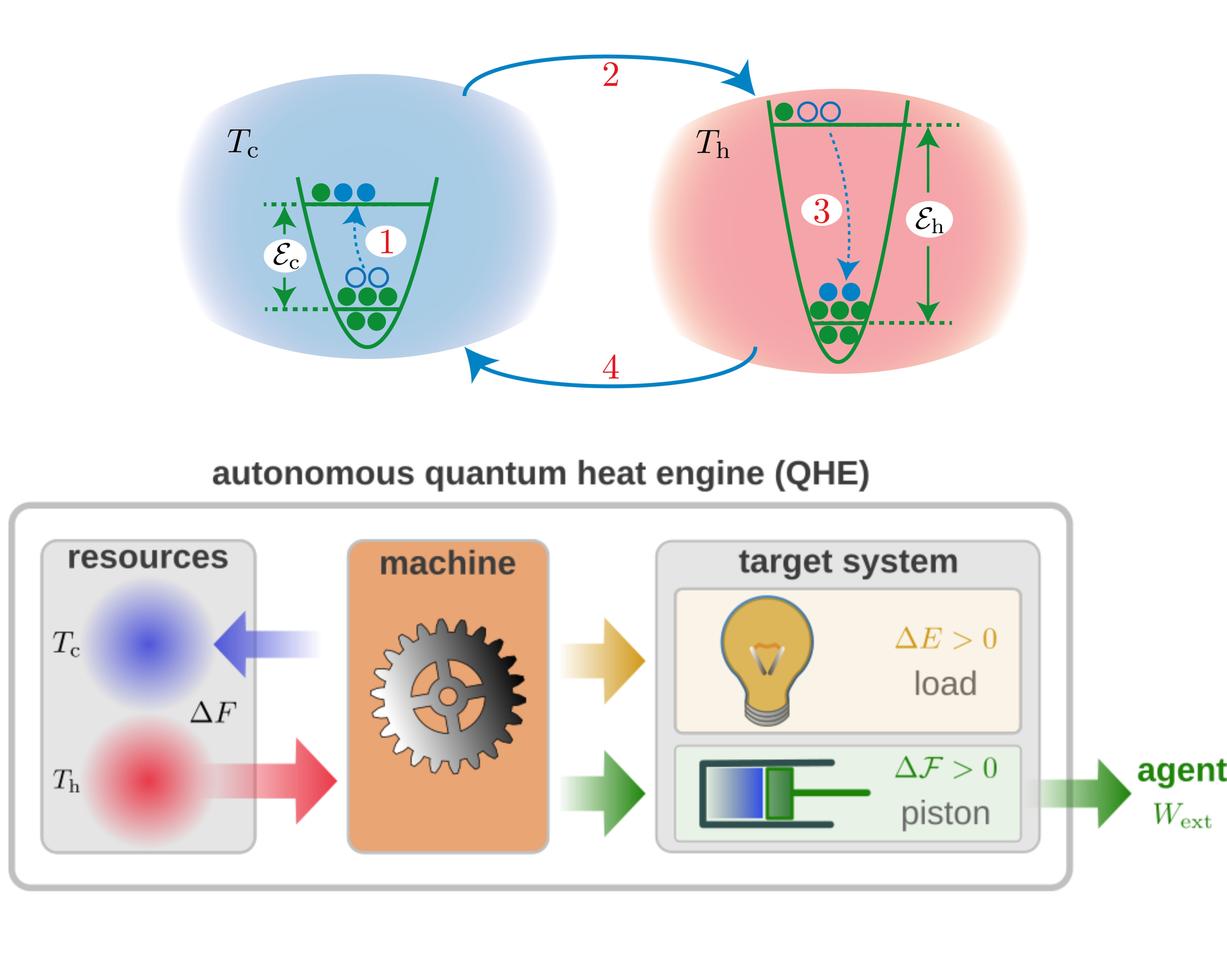
Quantum thermal machines
Quantum heat engines and refrigerators
Heat engines such as steam engines or internal combustion engines, are machines that convert thermal energy into mechanical work. The endeavour to increase their performance and efficiency has significantly contributed to the development of classical thermodynamics and the formalisation of its underlying laws. While thermodynamics is a macroscopic theory, the question whether, or to what extent, its rules translate to the microscopic, quantum, domain is a major driving force in the emerging field of quantum thermodynamics. In the thermodynamic tradition of "learning by example" the study of quantum thermal machines, e.g., refrigerators or heat engines, constituted by a few (or even a single) atoms, not only helps to answer those fundamental questions but is also aimed at identifying whether quantum features (like entanglement) may be beneficial for the operation of thermal machines.
Forces from thermal light and various subtleties of light-matter interaction
Attractive optical forces from black-body radiation
Quantum optics typically employs laser light to trap and manipulate atoms. But also localised sources of thermal radiation generate an environment, where atoms see a position-dependent Stark shifts, that is, a potential landscape. This leads to a weak, typically attractive force, pulling atoms towards hot objects. As this effect is measurable in atom interferometers, it has to be considered as an additional source of error in upcoming high-precision experiments. We also seek to explore how atoms interact collectively with thermal radiation in Bose-Einstein condensates or even astrophysical scenarios.
- M. Sonnleitner, M. Ritsch-Marte and H. Ritsch: Phys. Rev. Lett. 111, 023601 (2013)
- P. Haslinger, M. Jaffe, V. Xu, O. Schwartz, M. Sonnleitner, M. Ritsch-Marte, H. Ritsch and H. Müller:Nature Physics 14, 257 (2018)
A tale of two momenta
Light-matter interactions are full of subtle features which become relevant as experiments push the limits between "negligible" and "measurable". One of these subtleties is the Roentgen term which couples an atom to the magnetic component of a radiation field. Its physical interpretation is that a moving electric dipole (the atom) appears to have a magnetic dipole moment such that it can interact with magnetic fields as well. This term leads to a difference between the kinetic and the canonical momentum of an atom such that it might move differently than originally expected.

Towards a Superradiant Laser
The smallest possible laser
A single inverted atom in an optical micro resonator forms the smallest possible laser system as a coherent source of light. The laser light generated by the atom through stimulated emission exhibits strong forces which in turn provide for self-trapping and cooling of the atom. When operated on an ultra narrow clock transition one enters the super radiant operating regime which allows precise and accurate operation on the atomic clock transition wavelength. Our research in this field is embedded in the European Quantum Flagship iqClock Consortium.
- T. Maier, S. Kraemer, L. Ostermann and H. Ritsch: Optics Express 22, 11 (2014)
- C. Hotter, D. Plankensteiner, L. Ostermann and H. Ritsch: Optics Express 27, 31193 (2019)
- R. Holzinger, L. Ostermann and H. Ritsch: arXiv:1905.01483 (2019)
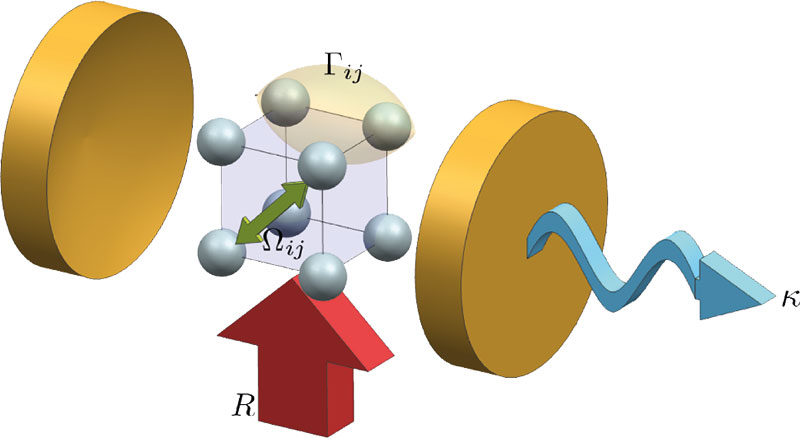
Protected subspace Ramsey spectroscopy
Quantum metrology: Making time measurements more precise
Quantum physics tells us that the energies an electron can have within an atom are directly associated with frequencies and can therefore be used to count time. This is usually done in an atomic clock, a setup that has been well established over the last 50 years.
As a matter of fact, atomic clocks have become that good that even the smallest interactions between atoms now constitute a perturbation that fundamentally limits the accuracy of such a device. In our work, we have suggested an alteration of the standard measurement procedure, the so-called Ramsey spectroscopy method, that leverages the unwanted interactions amongst the atoms and turns them into an advantage, yielding much better sensitivities and ultimately a more precise clock.
In a nutshell, the suggested alteration makes use of subradiant, i.e. slowly decaying states, that emerge as a consequence of the mutual dipole-dipole interaction amongst the atoms. Therby population can be retained much longer during the phase of free evolution during the Ramsey measurement procedure.
This, of course, has many applications ranging from fundamental physics over high-speed communications to improved GPS navigation and beyond.
- L. Ostermann, H. Ritsch and C. Genes: Phys. Rev. Lett. 111, 123601 (2013)
- L. Ostermann, C. Meignant, C. Genes and H. Ritsch: New J. Phys. 21, 025004 (2019)
QuantumOptics.jl: A Julia framework for simulating open quantum systems
Simulating the dynamics of open quantum systems
QuantumOptics.jl is an open source computational framework geared towards the efficient numerical investigation of open quantum systems written in the Julia programming language. Built exclusively in Julia and based on standard quantum optics notation, the toolbox offers speed comparable to low-level statically typed languages such as FORTRAN or C, without compromising on the accessibility and code readability found in dynamic languages.
More details, installation instructions and an extensive documentation with many examples can be found on the QuantumOptics.jl homepage.





